Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho hai đường thẳng xx' và yy' cắt nhau tại O. biết x'Oy+xOy'=120o. Tính các góc xOy;yOx';x'Oy';y'Ox


Ta có: 2 tia xx' và yy' cắt nhau tại O
\(\Rightarrow\widehat{xOy}\) và \(\widehat{yOx'}\) là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{yOx'}=180^0\)
Mà \(2\widehat{xOy}=3\widehat{yOx'}\Rightarrow\widehat{yOx'}=\dfrac{2}{3}\widehat{xOy}\)
\(\Rightarrow\widehat{xOy}+\dfrac{2}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\dfrac{5}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\widehat{xOy}=108^0\)

Số đo các góc tạo thành lần lượt là 120 độ; 120 độ; 60 độ và 60 độ

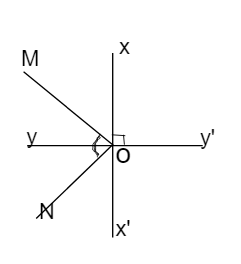
Vì xx' ⊥ yy' tại O (gt)
⇒ ∠x'Oy = 900 (định nghĩa 2 đường thẳng vuông góc)
Ta có: ∠xOy + ∠x'Oy = 1800 (2 góc kề bù)
Thay số: ∠xOy + 900 = 1800
∠xOy = 1800 - 900
∠xOy = 900
Mà OM là tia phân giác của ∠xOy
ON là tia phân giác của ∠yOx'
⇒ ∠mOy = 450
∠yOn = 450
Ta có: ∠mOy + ∠yOn = ∠mOn (2 góc kề nhau)
Thay số: 45+45 = ∠mOn
900 = ∠mOn
∠mOn = 900
Vậy ∠mOn = 900

a) Các cặp góc kề bù
\(\widehat{xOy}\) và \(\widehat{yOx'}\)
\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)
\(\widehat{xOy'}\) và \(\widehat{xOy}\)
Các cặp góc đối:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)
b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)
\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)
Hình vẽ:
Giải:
Vì xx' và yy' cắt nhau tại O
Nên \(\widehat{xOy}\) và \(\widehat{yOx'}\) là hai góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{yOx'}=180^0\)
Áp dụng tích chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{\widehat{xOy}}{2}=\dfrac{\widehat{yOx'}}{3}=\dfrac{\widehat{xOy}+\widehat{yOx'}}{2+3}=\dfrac{180^0}{5}=36^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{xOy}=36^0.2\\\widehat{yOx'}=36^0.3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{xOy}=72^0\\\widehat{yOx'}=108^0\end{matrix}\right.\)
Vì xx' và yy' cắt nhau tại O
Nên \(\widehat{xOy}\) và \(\widehat{yOx'}\) là hai góc đối nhau
\(\Rightarrow\widehat{xOy}=\widehat{x'Oy'}=72^0\)
Vậy \(\widehat{x'Oy'}=72^0\).
Chúc bạn học tốt!