Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc M1+góc M2=180 độ
3 góc M1-7 góc M2=0
=>góc M1=126 độ, góc M2=54 độ

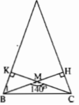
+) Xét tam giác vuông BKM có ∠BMC là góc ngoài tam giác tại đỉnh M nên:


1. Hai góc đối đỉnh thì bằng nhau, đúng
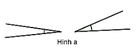
2. Hai góc bằng nhau thì đối đỉnh, sai
Vì tồn tại hai góc bằng nhau mà không chung đỉnh thì đó không phải hai góc đối đỉnh như hình sau:
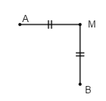
3. Nếu M là trung điểm của AB thì MA = MB, đúng
4. Nếu có MA = MB thì M là trung điểm của AB, sai
Vì nếu M, A, B không thẳng hàng thì MA = MB không suy ra được M là trung điểm của A
B.
5. Hai đường thẳng vuông góc thì cắt nhau, đúng
6. Hai đường thẳng cắt nhau thì vuông góc, sai
Vì hai đường thẳng cắt nhau không tạo thành góc vuông thì chúng không phải là hai đường thẳng vuông góc.
Chọn đáp án C

A B C I M N
Ta sử dụng tính chất: hai tia phân giác của hai góc kề bù thì vuông góc với nhau
+) BM; BI là 2 tia p/g của góc B trong và ngoài tam giác => BM | BI => góc MBI = 90o
CN và CI là 2 tia p/g của góc C trong và ngoài tam giác ABC => CN | CI => góc ICN = 90o
+) Xét tam giác MBC có: góc M + MCB + MBC = 180o => góc M + MCB + (MBI + IBC) = 180o
=> góc M + góc \(\frac{C}{2}\) + góc \(\frac{B}{2}\) + 90o = 180o => góc M + góc \(\frac{B+C}{2}\) = 90o => góc M = 90o - góc \(\frac{B+C}{2}\) = \(\frac{180^o-\left(B+C\right)}{2}=\frac{A}{2}\)
+) tương tự, ta có góc N = góc A/2
Vậy góc M = Góc N = góc A/2
b) đã làm ở bài trên

a: \(\widehat{MAQ}=180^0-60^0=120^0\)
\(\widehat{NAQ}=60^0\)

Gọi E là giao điểm của BM và AC, F là giao điểm của CM và AB
=>BM⊥AC tại E, CM⊥AB tại F
Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
\(\hat{FBC}=\hat{ECB}\)
Do đó: ΔFBC=ΔECB
=>\(\hat{FCB}=\hat{EBC}\)
=>\(\hat{MBC}=\hat{MCB}\)
=>ΔMBC cân tại M
=>\(\hat{MBC}=\hat{MCB}=\frac{180^0-\hat{BMC}}{2}=\frac{180^0-140^0}{2}=20^0\)
ΔEBC vuông tại E
=>\(\hat{EBC}+\hat{ECB}=90^0\)
=>\(\hat{ECB}=90^0-20^0=70^0\)
ΔBAC cân tại A
=>\(\hat{BAC}=180^0-2\cdot\hat{ACB}=180^0-2\cdot70^0=40^0\)
Trong tam giác nhọn \(A B C\) cân tại đỉnh \(A\), hai đường cao xuất phát từ đỉnh \(B\) và \(C\) cắt nhau tại \(M\). Dựa vào thông tin bài toán, ta sẽ giải quyết bài toán như sau:
Bước 1: Tính chất của tam giác cân
Do tam giác \(A B C\) là tam giác cân tại đỉnh \(A\), ta có:
\(A B = A C\)
Điều này đồng nghĩa với việc hai góc \(\angle A B C = \angle A C B\).
Bước 2: Đặc điểm của hai đường cao
Khi ta có hai đường cao \(B M\) và \(C M\) trong tam giác \(A B C\), điểm \(M\) là trực tâm của tam giác. Do đó, các góc liên quan đến trực tâm sẽ có một số tính chất đặc biệt.
Bước 3: Góc tại điểm M
Tại điểm \(M\), các đường cao \(B M\) và \(C M\) tạo thành một góc \(\angle B M C\). Theo bài toán, ta biết rằng:
\(\angle B M C = 140^{\circ}\)
Góc \(\angle B M C\) được tạo thành giữa hai đường cao, và trong tam giác nhọn \(A B C\), góc này có mối quan hệ với các góc ở các đỉnh của tam giác. Đặc biệt, ta có công thức sau cho tam giác nhọn:
\(\angle B M C = 180^{\circ} - \angle A\)
Bước 4: Giải phương trình
Ta thay giá trị \(\angle B M C = 140^{\circ}\) vào công thức trên:
\(140^{\circ} = 180^{\circ} - \angle A\)
Giải phương trình:
\(\angle A = 180^{\circ} - 140^{\circ} = 40^{\circ}\)
Kết luận:
Góc \(A\) của tam giác \(A B C\) bằng \(\boxed{40^{\circ}}\).