

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




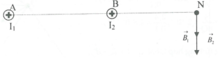
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ, cả hai dòng điện I1, I2 đi vào tại A và B.
a) M cách I1 và I2 khoảng 5cm.
Ta có d = AB = 10 cm; d1 = AM = 5 cm; d2 = BM = 5 cm.Suy ra M là trung điểm của đoạn AB.
Khi đó các dòng điện I1 và I2 gây ra tại M các vectơ cảm ứng từ B 1 → v à B 2 → có phương chiều như hình vẽ, có độ lớn:









Lời giải
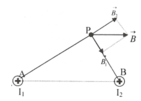
+ Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ, dòng I 1 đi vào tại , dòng I 2 đi vào tại . Các dòng điện I 1 và I 2 gây ra tại M các véc tơ cảm ứng từ B 1 và B 2
+ Để cảm ứng từ tổng hợp tại M bằng 0 thì B → = B → 1 + B → 2 ⇒ B → 1 = − B → 2 tức là và phải cùng phương, ngược chiều và bằng nhau về độ lớn. Để thỏa mãn cácđiều kiện đó thì M phải nằm trên đường thẳng nối A, B; nằm trong đoạn thẳng AB
Với B 1 = B 2
⇒ 2.10 − 7 . I 1 A M = 2.10 − 7 I 2 A B − A M ⇒ A M = A B . I 1 I 1 + I 2 = 10 c m ⇒ M B = 5 c m
Vậy điểm M phải nằm trên đường thẳng cách dây dẫn mang dòng I 1 và cách dây dẫn mang dòng I 2 cm.
Ngoài ra, còn có các điểm ở rất xa hai dây dẫn cũng có cảm ứng từ tổng hợp do hai dòng điện này gây ra cũng bằng 0 vì cảm ứng từ do mỗi dòng điện gây ra ở các điểm cách rất xa nó bằng 0
Chọn A

a)Hai dây dẫn cùng chiều.
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,05}=2\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,05}=4\cdot10^{-6}T\)
\(B=B_1+B_2=2\cdot10^{-5}+4\cdot10^{-6}=2,4\cdot10^{-5}T\)
b)Hai dây dẫn ngược chiều nhau.
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,05}=2\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,15}=1,33\cdot10^{-6}T\)
\(B=\left|B_1-B_2\right|=\left|2\cdot10^{-5}-1,33\cdot10^{-6}\right|=1,867\cdot10^{-5}T\)
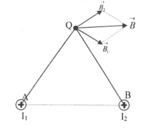
c)Hai dây dẫn vuông góc nhau (vì \(\sqrt{6^2+8^2}=10\))
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,06}=1,67\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,08}=2,5\cdot10^{-6}T\)
\(B=\sqrt{B_1^2+B_2^2}=\sqrt{\left(1,67\cdot10^{-5}\right)^2+\left(2,5\cdot10^{-6}\right)^2}=1,688\cdot10^{-5}T\)