K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
8 tháng 5 2018
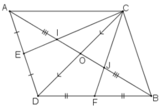
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB

18 tháng 5 2022
Gọi O là giao điểm của AB và CD
=>O là trung điểm chng của AB và CD
Xét ΔACD có
AO là đường trung tuyến
CE là đường trung tuyến
AO cắt CE tại I
Do đó: I là trọng tâm
=>AI=2/3AO=1/3AB(1)
Xét ΔCBD có
BO là đường trung tuyến
CF là đường trung tuyến
BO cắt CF tại J
Do đó; J là trọng tâm
=>BJ=2/3BO=1/3BA(2)
Từ (1) và (2) suy ra AI=BJ=1/3AB=JI
Xét tam giác ACD có AO, CE là hai đường trung tuyến cắt nhau tại I => I là trọng tâm => \(IO=\frac{1}{2}IA\) và \(IA=\frac{2}{3}OA\)
Tương tự: J là trong tâm tam giác BCD => \(OJ=\frac{1}{2}JE\) và \(JB=\frac{2}{3}OB\).
Theo giả thiết OA = OB => IA = JB và IJ = OI + OJ = AI = JB.
e cám ơn nhiều ạ