Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hiệu điện thế giữa 2 đầu điện trở R1 là :
\(U_1=I_1.R_1=2,2.25=55\left(V\right)\)
Hiệu điện thế giữa 2 đầu điện trở R2 là :
\(U_2=I_2.R_2=1,5.30=45\left(V\right)\)
Nếu R1//R2 thì :
\(U=U_1=U_2\)
=> U = 15V thì 2 điện trở ko phù hợp để mắc song song.

Tóm tắt :
\(R_1=4\Omega\)
\(R_2=6\Omega\)
R1 nt R2
\(U=12V\)
_____________________________________
Rtđ = ?
I1 = ?; I2 = ?
U1 = ? ; U2 = ?
GIẢI :
Vì R1 nt R2 nên :
Điện trở tương đương toàn mạch là :
\(R_{tđ}=R_1+R_2=4+6=10\left(\Omega\right)\)
Cường độ dòng điện qua mạch chính là :
\(I_{mc}=\dfrac{U}{R_{tđ}}=\dfrac{12}{10}=1,2\left(A\right)\)
=> I1 = I2 = Imc = 1,2A (do R1 nt R2)
Hiệu điện thế hai đầu điện trở R1 là :
\(U_1=I_1.R_1=1,2.4=4,8\left(V\right)\)
Hiệu điện thế hai đầu R2 là :
\(U_2=I_2.R_2=1,2.6=7,2\left(V\right)\)

Tóm tắt :
\(U=8V\)
\(I=0,2A\)
\(R_1=3R_2\)
\(R_1=?,R_2=?\)
Lời giải : Điện trở tương đương của đoạn mạch là :
\(R_{tđ}=\dfrac{U}{I}=\dfrac{8}{0,2}=40\Omega\)
Mà \(R_1ntR_2\Rightarrow R_1+R_2=40\Omega\)
Từ đó ta có hệ : \(\left\{{}\begin{matrix}R_1=3R_2\\R_1+R_2=40\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}R_1=30\Omega\\R_2=10\Omega\end{matrix}\right.\)

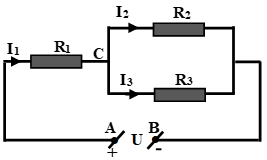
a) \(R_1nt(R_2//R_3)\)
\(R_1=\dfrac{U_1}{I_1}\Rightarrow U_1=0,4.14=5,6\left(V\right)\)
\(I_1=I_{AB}=0,4A\)
Có \(R_{AB}=R_1+R_{23}=14+\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{434}{19}\left(\Omega\right)\)
\(\Rightarrow U_1+U_{23}=U_{AB}=R_{AB}.I_{AB}=\dfrac{439}{19}.0,4=\dfrac{868}{95}\left(V\right)\)
\(\Rightarrow U_{23}=\dfrac{868}{95}-5,6=\dfrac{336}{95}\left(V\right)\)
\(\Rightarrow U_2=U_3=\dfrac{336}{95}\left(V\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{24}{95}\left(A\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{14}{95}\left(V\right)\)
b) \(U_{AB}=\dfrac{868}{95}\left(V\right)\)
\(U_{AC}=I_1.R_1=0,4.14=5,6\left(V\right)\)
\(U_{CB}=I_{23}.R_{23}=0,4.\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{336}{95}\left(V\right)\)
Vậy...

khi mắc nối tiếp: \(R_t=R_1+R_2=50\Omega\)
Khi mắc song song: \(R_t=\dfrac{R_1.R_2}{R_1+R_2}=12,5\Omega\)
\(\Rightarrow R_1.R_2=12,5.50=625\Omega\)
\(\Rightarrow\left\{{}\begin{matrix}R_1=50-R_2\\\left(50-R_2\right).R_2=1800\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}R_1=50-R_2\\R_2^2-90R_2+1800=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}R_1=90-R_2\\\left\{{}\begin{matrix}R_2=30\\R_2=60\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}R_1=60\\R_2=30\end{matrix}\right.\\\left\{{}\begin{matrix}R_1=30\\R_2=60\end{matrix}\right.\end{matrix}\right.\)

Tóm tắt :
\(R_1=15\Omega\)
\(R_2=10\Omega\)
R1//R2
\(U=12V\)
a) Rtđ = ?
b) t = 15' = 900s
Q = ?
GIẢI :
a) Điện trở tương đương của mạch là :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{15.10}{15+10}=6\left(\Omega\right)\)
b) \(I=\dfrac{U}{R_{tđ}}=\dfrac{12}{6}=2\left(A\right)\)
Nhiệt lượng tỏa ra trên đoạn mạch :
\(Q=I^2.R.t=2^2.6.900=21600\left(J\right)\)