Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để hệ 3 điện tích cân bằng thì lực điện tác dụng lên 2 điện tích bắt kì tác dụng lên điện tích còn lại phải bằng 0.
Để q3 cân bằng thì F23=F13 = \(\dfrac{k\left|q_1q_3\right|}{r^2_{1^{ }}}=\dfrac{k\left|q_2q_3\right|}{r^2_2}\left(1\right)\)
=> Điện tích q3 mang dấu âm, nằm ngoài khoảng q1,q2 và gần q1 hơn (Vì nằm gần vị trí điện tích có độ lớn lớn hơn)
Từ (1) => \(\dfrac{r1}{r2}=\sqrt{\dfrac{q1}{q2}}=\dfrac{1}{3}\)
Có: r2 - r1 =12 => r1=6 cm, r2=18 cm.
Để q1 cân bằng thì F31 = F21 khai triển và thay số ta được : q3 = -4,5.10-8 C.

đáp án A
+ Các điện tích q1 và q2 tác dụng lên điện tích q các lực F1 và F2 có phương chiều như hình vẽ, có độ lớn lần lượt:
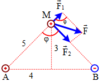
F 1 = k q 1 q r 2 = 9 . 10 9 . 10 - 8 . 10 - 8 0 , 05 2 = 3 , 6 . 10 - 4 N F 2 = k q 2 q r 2 = 9 . 10 9 . - 3 . 10 - 8 . 10 - 8 0 , 05 2 = 10 , 8 . 10 - 4 N
⇒ F = F 1 2 + F 2 2 - 2 F 1 F 2 cos φ → F = 12 , 3 . 10 - 4 N

Chọn đáp án A
Để hệ 3 điện tích cân bằng thì lực điện do 2 điện tích bất kì tác dụng lên điện tích còn lại phải bằng 0