Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Sử dụng công thức tính góc quét được trong thời gian ∆t: α = ω.∆t
Cách giải:
Lúc t = 0, vì 2 vật có cùng biên độ, cùng đi qua vị trí cân bằng theo chiều dương nên M trùng N. Khi hai vật đi ngang qua nhau, vì chu kỳ của M lớn hơn nên M đi chậm hơn. Ta có: αN + αM = π (1)
Và theo bài cho ta có:
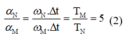
Từ (1) và (2) ta có:
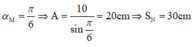

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Đáp án A
Ta có
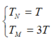
Giả sử M,N cùng đi qua VTCB theo chiều âm, ta có
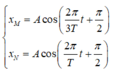
Khi chúng gặp nhau thì :
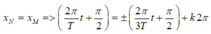
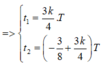
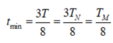
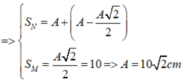
![]()

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

Chọn C


Lúc t = 0 hai chất điểm qua VTCB theo chiều dương (vị trí M 1 , M 2 như hình).
Hai chất điểm gặp nhau ngay sau đó khi chúng ở vị trí M 1 ' , M 2 ' như hình.
![]()

Đáp án C
Ban đầu hai chất điểm đang ở vị trí cân bằng và chuyển động theo chiều dương nên đường tròn lượng giác chúng ở vị trí M 0
Ta có ω N = 5 ω M nên khi gặp nhau thì M và N đã quét được các góc φ và 5 φ
Do đối xứng qua Ox nên dễ dàng tìm được φ = 30 o
Khi đó