
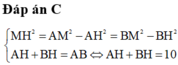
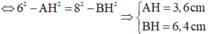

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

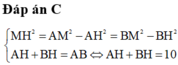
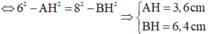


Đáp án C
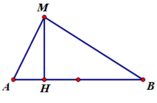
Dễ tìm chứng minh được tam giác MAB vuông tại M.
Có A H = M A 2 A B = 3 , 6 ( c m ) ; B H = M B 2 A B = 6 , 4 ( c m )
Số đường cực đại cắt qua MH là nghiệm k của bất pt:
A H − B H λ ≤ k ≤ A M − B M λ ⇔ − 0 , 93 ≤ k ≤ − 0 , 67 . Vì k nguyên nên bất pt này vô nghiệm. Vậy không có đường cực đại nào cắt MH.

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

Số đường hyperbol cực đại cắt MN bằng số điểm cực đại trên CD
+Ta có AM – BM = AC – BC = 7cm
Và AC + BC = AB = 13cm suy ra AC = 10cm
+Ta lại có AM2 – AD+2 = BM2 – DB2
Và DB = AB – AD suy ra AD = 11,08cm
+Xét một điểm bất kì trên AB, điều kiện để điểm đó cực đại là :
\(d_2-d_1=k\lambda;d_2+d_1=AB\Rightarrow d_2=\frac{\left(AB+k\lambda\right)}{2}\)
+ số điểm cực đại trên AC là: \(0\le d_2\le AC\Leftrightarrow0\le\)\(\frac{AB+k\lambda}{2}\le AC\Leftrightarrow-\frac{AB}{\lambda}\le k\le\)\(\frac{2AC-AB}{\lambda}\)
\(\Leftrightarrow-10,8\le k\le5,8\Rightarrow\) có 16 điểm cực đại
+ số cực đại trên AD: \(0\le d_2\le AD\Leftrightarrow0\le\frac{AB+k\lambda}{2}\le AD\Leftrightarrow\)\(-\frac{AB}{\lambda}\le k\le\frac{2AD-AB}{\lambda}\)
\(\Leftrightarrow-10,8\le k\le7,6\Rightarrow\) có 18 điểm cực đại
Vậy trên CD có 18 – 16 = 2 cực đại, suy ra có 2 đường hyperbol cực đại cắt MN.
\(\rightarrow\) Chọn C


Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A

Đáp án B
Ta có ![]() nên tam giác AMB vuông tại M.
nên tam giác AMB vuông tại M.
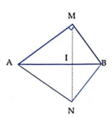
Mà ![]() suy ra IB= 9 cm.
suy ra IB= 9 cm.
Xét trên đoạn IM, số điểm dao động với biên độ cực đại là
![]() . Vậy trên đoạn IM có 1 điểm dao động với biên độ cực đại.
. Vậy trên đoạn IM có 1 điểm dao động với biên độ cực đại.
Do tính chất đối xứng IN cũng có một điểm dao động với biên độ cực đại.
Vậy trên MN có 2 điểm dao động vơi biên độ cực đại.