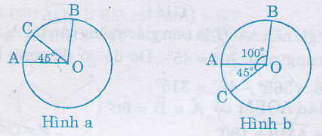Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Trong tứ giác AOBM có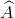 
= 
= 
.
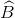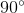Suy ra cung AMB + 
= 
=> cung AMB= -
= - 
= 
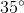
b) Từ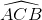 
= . Suy ra số đo cung nhỏ AB = và số đo cung lớn AB :
Cung AB =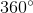 
- = 
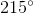
O C F A E B M P Q 1
+) Bước 1: Chứng minh \(\Delta\) FPO vuông tại P
Ta có: \(\widehat{O_1}=\widehat{FOP}=\widehat{FOE}=\widehat{FOM}+\widehat{MOE}=\frac{1}{2}\widehat{COM}+\frac{1}{2}\widehat{MOB}=\frac{1}{2}\widehat{BOC}\)
=> \(\widehat{FOP}=\frac{1}{2}\widehat{BOC}\)
mà \(\widehat{FCP}=\widehat{FCB}=\frac{1}{2}\widehat{BOC}\) ( góc nội tiếp = 1/2 góc ở tâm khi chắn cùng một cung)
=> \(\widehat{FOP}=\widehat{FCP}\)
=> Tứ giác CFPO nội tiếp => \(\widehat{FPO}+\widehat{FCO}=180^o\Rightarrow\widehat{FPO}=180^o-90^o=90^o\)
=> \(\Delta\) FPO vuông tại P
+) Bước 2: Chứng minh \(\Delta\) EQO vuông tại Q. ( Chứng minh tương tự)
+) Bước 3: Chứng minh tỉ số: \(\frac{PQ}{EF}=\frac{OQ}{OE}\)
Xét \(\Delta\) FPO vuông tại P và \(\Delta\) EQO vuông tại Q có: \(\widehat{O_1}\) chung
=> \(\Delta\) FPO ~ \(\Delta\) EQO
=> \(\frac{OQ}{OE}=\frac{OP}{OF}\)
Xét \(\Delta\) OQP và \(\Delta\) OEF có: \(\frac{OQ}{OE}=\frac{OP}{OF}\)( chứng minh trên ) và \(\widehat{O_1}\) chung
=> \(\Delta\) OQP ~ \(\Delta\) OEF
=> \(\frac{PQ}{EF}=\frac{OQ}{OE}\)(1)
+) Bước 4: Chứng minh Tỉ số \(\frac{PQ}{EF}\)không đổi khi M di chuyển trên cung nhỏ BC
Xét \(\Delta\)EQO vuông tại Q => \(\cos\widehat{O_1}=\frac{OQ}{OE}\)
Mặt khác : \(\widehat{O_1}=\frac{1}{2}\widehat{BOC}\) ( xem chứng minh ở Bước 1)
=> \(\cos\frac{1}{2}.\widehat{BOC}=\frac{OQ}{OE}\) (2)
Từ (1) ; (2) => \(\frac{PQ}{EF}=\cos\frac{1}{2}.\widehat{BOC}\)không đổi khi M di chuyển. ::))
+) Có A,B thuộc đường tròn (O;R)
=> OA = OB = R Mà AB = R
=> OA = OB = AB => tam giác AOB đều ( định nghĩa tam giác đều)
=> góc AOB = 60 độ ( tính chất tam giác đều)
Trong đường tròn (O;R) có góc AOB là góc ở tâm chắn cung AB nhỏ
=> số đo cung AB nhỏ = góc AOB = 60 độ (tính chất góc ở tâm )
+) Có B,C thuộc đường tròn (O;R) => OB=OC=R
Có OB^2 + OC^2 = R^2 + R^2= 2*R^2 = BC^2 ( vì BC = R\(\sqrt{2}\) )
=> tam giác BOC vuông ở O ( định lý Py-ta-go đảo )
=> góc BOC = 90 độ
Trong đường tròn (O;R) có góc BOC là góc ở tâm chắn cung BC nhỏ
=> góc BOC = số đo cung BC nhỏ ( tính chất góc ở tâm) => số đo cung BC nhỏ = 90 độ
+) Vì tia BO nằm giữa 2 tia BA và BC nên B nằm giữa A và C
=> số đo cung AB nhỏ + số đo cung BC nhỏ = số đo cung AC nhỏ
=> số đo cung AC nhỏ = 60 độ + 90 độ = 150 độ
k cho mk nha !!!!!!!!!!!
a) Ta có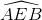 
là góc có đỉnh ở bên ngoài đường tròn nên:
\(\widehat{AEB}=\dfrac{sđ\left(\widehat{AB}-\widehat{CD}\right)}{2}=\dfrac{180^O-60^O}{2}=60^O\)
và \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:
\(\widehat{BTC}\) = sđ\(\dfrac{\widehat{BAC}-\widehat{BDC}}{2}=\dfrac{\left(180^O+60^O\right)-\left(60^O+60^O\right)}{2}=60^O\)
Vậy =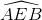
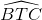
b) \(\widehat{DCT}\) là góc tạo bởi tiếp tuyến và dây cung nên:
\(\widehat{DCT}=\dfrac{sđ\widehat{CD}}{2}=\dfrac{60^o}{2}=30^o\)
→ \(\widehat{DCB}\) là góc nội tiếp trên
\(\widehat{DCB}\) = \(\dfrac{sđ\widehat{DB}}{2}\) = \(\dfrac{60^O}{2}=30^O\)
Vậy \(\widehat{DCT}\) = \(\widehat{DCB}\) hay CD là phân giác của \(\widehat{BCT}\)
a: góc AOC; góc BOD; góc AOD; góc BOC
b: góc COB=góc AOD=60 độ
=>sđ cung BC=60 đọ
góc AOC=180-60=120 độ
=>sđ cung AC=120 độ
c: sđ cung AC>sđ cung AD
=>AD>AC
a) Điểm C nằm trên cung nhỏ AB ( hình a)
Số đo cung nhỏ BC = 100º – 45º = 55º
Số đo cung lớn BC = 360º – 55º = 305º
b) Điểm C nằm trên cung lớn AB (hình b)
Số đo cung nhỏ BC = 100º + 45º = 145º
Số đo cung lớn BC = 360º – 145º = 215º
