Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Từ đồ thị ta thấy rằng hai dao động này này vuông pha nhau (động năng của vật 1 cực đại – đang ở vị trí cân bằng, thì động năng của vật 2 cực tiểu – đang ở biên) và E 1 = 1 , 5 E 2 .
+ Ta biểu diễn động năng và thế năng của các vật về cơ năng


Vẽ vòng tròn ta ta có thể thấy được vị trí góc pha mà thế năng bằng động năng là
\(\varphi=\left(2k+1\right)\frac{\pi}{4}\)
Cứ sau góc \(\frac{\pi}{2}\) thì thế năng bằng động năng tương ứng với T/4
hu kỳ dao động là T = 0.2s suy ra \(\omega=10\pi\)
\(k=\omega^2m=\frac{50N}{m}\)

Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)

Tần số dao động: \(f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{36}{0,1}}=3Hz\)
Trong dao động điều hòa, động năng và thế năng biến thiên với tần số gấp đôi tần số dao động.
\(\Rightarrow f'=2.3=6Hz\)

Tại thời điểm giữ lò xo thì: \(W_{d}=W_{t}=\dfrac{W}{2}\)
Cố định 1 điểm chính giữa lò xo thì thế năng giảm đi 1 nửa
\(\Rightarrow W_{t'}=\dfrac{W_t}{2}=\dfrac{W}{4};W_{đ}=\dfrac{W}{2}\Rightarrow W'=\dfrac{3W}{4}\)
Có: \(k'=2k\Rightarrow \dfrac{3}{4}.kA^{2}=k'A'^{2}\)
\(\Rightarrow \dfrac{A}{A'}=\dfrac{4}{\sqrt{6}}\)

\(t=0\Rightarrow x_1=4\cos\dfrac{\pi}{3}=2(cm)\)
\(t=\dfrac{T}{6}\Rightarrow x_2=-2cm\)
Do \(x_1=x_2\Rightarrow W_{t1}=W_{t2}\Rightarrow W_{đ1}=W_{đ2}\)
Như vậy tỉ số động năng bằng 1.

Trong dao động điều hòa, động năng và thế năng biến thiên tuần hoàn với tần số gấp đôi tần số của dao động.
\(f_2=2.2f_1=4f_1\)
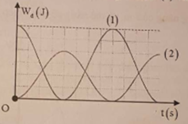
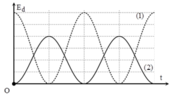

Phương pháp: Sử dụng định luật bảo toàn cơ năng kết hợp kĩ năng đọc đồ thị
Cách giải: Từ đồ thị ta có:
*Hai dao động cùng tần số và vuông pha nhau nên
Khi thế năng của hai con lắc bằng nhau ta có:
tỉ số động năng con lắc (2) và động năng con lắc (1) là:
Đáp án C