
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

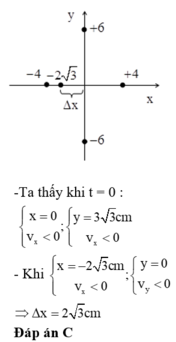
Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

Tại những điểm cách O một đoạn x thì biên độ giảm \(2.5\sqrt{x}\)lần
=> biên độ tại điểm M cách O một đoạn 25cm là \(\frac{2}{2,5.\sqrt{25}} = 0.16cm. \)
M trễ pha hơn O:
\(u_M=0.16\cos(4\pi t - 2\pi\frac{OM}{\lambda})= 0.16\cos(40\pi t - \frac{5\pi}{3})cm.\)