Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Dung kháng của tụ là \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \).

Khi trong mạch xảy ra cộng hưởng thì ω = ${\omega _0} = \dfrac{1}{{\sqrt {LC} }}$.

a+b
Đ1 Đ2
C) Do đây là mạch điện mắc nối tiếp => Ia = I1 = I2 => Cường độ dòng điện chạy qua đèn 1 = cường độ dòng điện chạy qua đèn 2 = 2A

trong trường hợp ban đầu
điện áp R cực đại nên tại f1 xảy ra hiện tượng cộng hưởng
\(Z_L=Z_C\)
\(LC=\frac{1}{\omega^2_1}\)
Trong trường hợp sau thì điện áp AM không đổi khi thay đổi R, lúc cố định tần số nghĩa là cảm kháng và dung kháng đều cố định
như vậy thì chỉ có trường hợp duy nhất là Uam bằng với U
Khi đó
\(Z_{LC}=Z_L=Z_C-Z_L\)
\(Z_C=2Z_L\)
\(LC=\frac{1}{2\omega^2_2}\)
Suy ra
\(\omega^2_1=2\omega^2_2\)
\(f_1=\sqrt{2}f_2\)

Câu 1: \(e_c=\dfrac{L\Delta i}{\Delta T}=0,005.0,4=0,002V\)
Chọn C.
Câu 2. Cường độ dòng điện: \(I=9:(8+1)=1A\)
Khối lượng đồng bán vào ca tốt trong 5h là:
\(m=\dfrac{1}{96500}.\dfrac{64}{2}.1.5.3600=5,97g\)
Chọn A
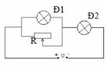


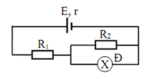
Chọn D
Đèn 1 và 2 sáng bình thường nên U 1 =6V; U 1 =8V
Theo hình vẽ Đ2 nt (Đ1//biến trở)
U= U 1 + U 2 =6+8=14V
Trong các đáp án chỉ có đáp án D có U=14V nên ta loại trừ các đáp án khác.
Chọn D là đáp án đúng.