Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là vận tốc của ca nô ( km/h; x>0)
Vận tốc ca nô đi xuôi : x+3
Vận tốc ca nô đi ngược: x-3
Thời gian ca nô đi xuôi từ A đến B là: \(\dfrac{40}{x+3}\left(h\right)\)
Thời gian ca nô đi ngược từ B đến khi gặp bè là: \(\dfrac{32}{x-3}\left(h\right)\)
Thời gian bè trôi đến khi gặp ca nô là \(\dfrac{8}{3}\)
Ta có pt: \(\dfrac{40}{x+3}+\dfrac{32}{x-3}=\dfrac{8}{3}\)
\(\Leftrightarrow120\left(x-3\right)+96\left(x+3\right)-8\left(x+3\right)\left(x-3\right)\Leftrightarrow8x^2-216x=0\Leftrightarrow x=27\)(tmđk) Vậy vận tốc của ca nô là 27km/h

Gọi vận tốc ca nô là x(km/h), x > 3. Vận tốc ca nô xuôi dòng là x + 3(km/h)
Thời gian ca nô xuôi dòng từ A đến B là 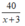 (giờ)
(giờ)
Vận tốc ca nô ngược dòng là x - 3 (km/h)
Quãng đường ca nô ngược dòng từ B đến địa điểm gặp bè là : 40 - 8 = 32 km
Thời gian ca nô ngược dòng từ B đến địa điểm gặp bè là: 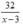 (giờ)
(giờ)
Thời gian bè trôi là:
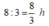
Ta có phương trình:
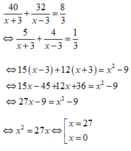
So sánh với điều kiện thì chỉ có nghiệm x = 27 thỏa mãn, suy ra vận tốc của ca nô là 27km/h.
Chọn đáp án C

Gọi x (km/h) là vận tốc thực của ca nô (x>4)
Vận tốc xuôi dòng của ca nô là : x + 4 (km/h)
Vận tốc ngược dòng của ca nô là : x - 4 (km/h)
Thời gian ca nô đi gặp bè nứa: 8 : 4 = 2 (giờ )
Thời gian xuôi dòng của ca nô là : \(\frac{24}{x+4}\)(giờ)
Thời gian ngược dòng đến chỗ gặp bè nứa của ca nô là \(\frac{16}{x-4}\)(giờ)
Ta có phương trình : \(\frac{24}{x+4}+\frac{16}{x-4}=2\)
Giaỉ phương trình ta được : \(x_1=20;x_2=0\left(lọai\right)\)
Vận tốc thực của ca nô là : 20km/h

Gọi x,y lần lượt là vận tốc của ca nô và dòng nước.
Do bè nứa trôi tự do nên vận tốc của bè nứa bằng vận tốc của dòng nước.
Tổng thời gian đi là 14 giờ.
- Vận tốc xuôi dòng là x + y
- Vận tốc ngược dòng là x - y
=> Ta có PT:
96/x+y + 96/x−y= 14 (*)
Lúc ca nô gặp bè nứa, tức là ca nô đi được 96 km xuôi dòng, 96 - 24 = 72 km ngược dòng, tốn hết quãng thời gian bằng với bè nứa trôi với vận tốc y được 24 km
=> Ta có PT
96/x+y + 72/x−y = 24y (**)
Giải hệ phương trình (*) và (**) ta được:
x = 14
y = 2
Vậy:
- Vận tốc riêng của ca nô là 14 km/h
- Vận tốc riêng của dòng nước là 2 km/h.
@maiban5d : bạn giải phương trình (*) với (**) hộ mình với :)

Gọi A là vị trí mà tại đó ca nô vượt qua bè, v1 là vận tốc của ca nô so với nước, v2 là vận tốc của dòng nước.
Trong thời gian t1 = 45’ = 0,75(h) ca nô đi được quãng đường là :
AC = ( v1 + v2 )t1. trong thời gian đó bè trôi được quãng đường AD = v2t1.
Khi ca nô quay lại thì khoảng cách giữa ca nô và bè là: CD =AC - AD
=> CD = (v1+v2)t1 - v2t1
= v1t1 + v2t1 - v2t1
= v1t1 (1)
Giả sử bè và ca nô gặp nhau tại E, ta có : EB = 6 km
Gọi t là thời gian ca nô và bè đi để gặp nhau kể từ lúc ca nô quay lại, ta có:
t = CD/(v1-v2)+v2
= CD/v1
=> CD = v1t (2)
Từ (1) và (2) => t = t1 = 0,75 (h)
Theo đề bài ta có:AD +DE + EB = 15(km) và EB = 6 (km)
AD +DE = 15 - 6 = 9 (km) = AE và AE là quãng đường bè trôi trong thời gian t’ = t + t1 = 0,75 + 0,75 = 1,5 (h)
Vậy vận tốc của dòng nước là:
v2 = AE/t' = 9/1,5 = 6 (km/h)

Lời giải:
Gọi vận tốc cano lúc yên lặng là $x$ km/h thì vận tốc xuôi dòng là $x+3$ km/h và vận tốc xuôi dòng là $x-3$ km/h
Tổng thời gian đi lẫn về là:
$\frac{60}{x+3}+\frac{60}{x-3}=11h-7h=4$ (h)
Giải pt trên với điều kiện $x>3$ ta suy ra $x\approx 30,3$ (km/h)
Nhiều bài thế :) đăng không biết mỏi hã bạn
Gọi x là vận tốc của chiếc ca nô
vân tốc ca nô xuôi dòng là x + 3 ( km/h )
vận tốc ca nô ngược dòng là x - 3 ( km/h )
Thời gian ca nô xuôi dòng là \(\frac{40}{x+3}\)
Thời gian ca nô ngược dòng là \(\frac{40-8}{x-3}\)
Theo đề bài ta có phương trình:
\(\frac{40}{x+3}+\frac{40-3}{x-3}=\frac{8}{3}\)
\(\Leftrightarrow\frac{40}{x+3}+\frac{32}{x-3}=\frac{8}{3}\)
\(\Leftrightarrow8x^2-126x=0\Leftrightarrow\hept{\begin{cases}x=0\\x=27\left(tmđk\right)\end{cases}}\)( x = 0 không thỏa mãn điều kiện )
Vậy vân tốc ca nô là 27 km/h
Trả lời
Gọi x là vận tốc của chiếc ca nô
x+3 là ca nô xuôi dòng
x-3 là cano ngược dòng
Mà một chiếc bè cùng trôi từ A đến B với vận tốc 3km/h => vận tốc xuôi dòng
40 / (x+3) là thời gian đi từ A --> B
32 / (x-3) là thời gian đi từ B --> A gặp chiếc bè trôi
3:8 Là thời gian bè trôi cũng là thời gian ca no gặp chiếc bè
Ta có pt :
40 / (x+3) + 32 (x-3) = 8:3
Giải từ từ thì vận tốc của ca nô là 27 km/h
~Hok tốt~