Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi thời gian mở vòi chảy để số nước còn lại ở bể thứ nhất bằng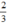 
số nước ở bể thứ hai là x (phút) (x > 0)
Lượng nước đã chảy đi khỏi bể thứ nhất là 15x (lít)
Lượng nước đã chảy đi khỏi bể thứ hai là 25x (lít)
Lượng nước còn lại ở bể thứ nhât là 800 – 15x (lít)
Lượng nước còn lại ở bể thứ hai là 1300 – 25x (lít)
Theo bài ra ta có phương trình:
800 – 15x =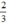 
(1300 – 25x)
⇔ 2400 – 45x = 2600 – 50x
⇔ 5x = 200
⇔ x = 40 (tmđk)
Vậy sau 40 phút số nước còn lại ở bể thứ nhất bằng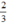 
số nước còn lại ở bể thứ hai.
ĐS: 40 phút.
Goi x là thời gian để số nước còn lại ở bể thứ 1 bằng 2/3 số nước còn lại ở bể thứ 2.
sau thời gian x,lượng nước còn lại ở bể thứ nhất:800-15x
sau thời gian x,lượng nước còn lại ỏ bể thứ hai:1300-25x
vì theo đề ra số nước còn lại ở bể thứ nhất bằng 2/3 lần số nước ở bể thứ 2 nên ta có phương trình
Goi x là thời gian để số nước còn lại ở bể thứ 1 bằng 2/3 số nước còn lại ở bể thứ 2.
Theo đề bài ta có:
\(\left(800-15x\right)=\frac{2}{3}\left(1300-25x\right)\)
\(x=40\)
Ghọi thời gian hai vời chảy đến khi lượng nước còn lại ở bể một bằng 2/3 lượng nước còn lại ở bể hai là : \(x\)phút
lượng nước đã chảy của bể một là : \(15x\)lít
lượng nước còn lại trong bể một :\(800-15x\)lít
Lượng nước đã chảy của bể hai: \(25x\)lít
Lượng mước còn lại trong bể hai : \(1300-25x\)lít
theo giả thết có phương trình :
\(800-15x=\frac{2}{3}\left(1300-25x\right)\)
\(\Leftrightarrow2400-45x=2600-50x\)
\(\Leftrightarrow5x=200\Leftrightarrow x=40\)
Đs :\(40\)phút
a) Ở đây thứ biến đổi là giờ, nên ta gọi giờ là x
8 giờ bể giảm 18 lít => 1 giờ giảm 2,25
Lượng ước trong bể: f(x) = 100 - x*2,25.
b) Áp dụng phương trình hàm số tìm được ở câu a.
c) bể còn lại 34 lít => f(x) = 34, thay ngược vào phương trình hàm số câu a là ra.
Chúc em học tốt!
Gọi thời gian số nước còn lại trong bể thứ nhất bằng \(\dfrac{2}{3}\) số nước còn lại trong bể thứ hai là \(x\left(phút\right)\left(x>0\right)\)
Khi đó:
- Bể thứ nhất chảy đi \(24x\left(l\text{ nước }\right)\), còn lại \(1200-24x\left(l\text{ nước }\right)\)
- Bể thứ nhất chảy đi \(32x\left(l\text{ nước }\right)\), còn lại \(1650-32x\left(l\text{ nước }\right)\)
Vì sau \(x\left(phút\right)\) số nước còn lại trong bể thứ nhất bằng \(\dfrac{2}{3}\) số nước còn lại trong bể thứ hai
nên ta có phương trình :
\(1200-24x=\dfrac{2}{3}\left(1650-32x\right)\\ \Leftrightarrow1200-24x=1100-\dfrac{64}{3}x\\ \Leftrightarrow-24x+\dfrac{64}{3}x=1100-1200\\ \Leftrightarrow-\dfrac{8}{3}x=-100\\ \Leftrightarrow x=\dfrac{75}{2}\left(T/m\right)\)
Vậy thời gian số nước còn lại trong bể thứ nhất bằng \(\dfrac{2}{3}\) số nước còn lại trong bể thứ hai là \(\dfrac{75}{2}\left(phút\right)\)