Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

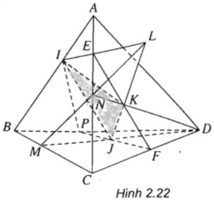
a) Gọi N = DK ∩ AC; M = DJ ∩ BC.
Ta có (DJK) ∩ (ABC) = MN ⇒ MN ⊂ (ABC).
Vì L = (ABC) ∩ JK nên dễ thấy L = JK ∩ MN.
b) Ta có I là một điểm chung của (ABC) và (IJK).
Mặt khác vì L = MN ∩ JK mà MN ⊂ (ABC) và JK ⊂ (IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK) ∩ (ABC) = IL.
Gọi E = IL ∩ AC; F = EK ∩ CD. Lí luận tương tự ta có EF = (IJK) ∩ (ACD).
Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).
Ta có PF = (IJK) ∩ (BCD) Và IP = (ABD) ∩ (IJK)

a) Gọi \(N=DK\cap AC;M=DJ\cap BC\).
Ta có \(\left(DJK\right)\cap\left(ABC\right)=MN\Rightarrow MN\subset\left(ABC\right)\)
Vì \(L=\left(ABC\right)\cap JK\) nên dễ thấy \(L=JK\cap MN\)


1) Bài toán trọng tâm của tứ diện:
A B C D G E F H K M N
Ta có NE,MF lần lượt là đường trung bình của \(\Delta ABC,\Delta ADC\), suy ra \(\hept{\begin{cases}NE=MF=\frac{AC}{2}\\NE||MF\end{cases}}\)
Suy ra tứ giác EMFN là hình bình hành. Do đó EF,MN cắt nhau tại trung điểm của mỗi đoạn.
Tương tự MN,HK cũng cắt nhau tại trung điểm của mỗi đoạn.
Vậy EF,HK,MN đồng quy tại trung điểm G của chúng. G chính là trọng tâm của tứ diện ABCD.
*) Nhận xét: Ta dễ dàng chỉ ra:
i) AG,BG,CG,DG lần lượt đi qua trọng tâm GA,GB,GC,GD của các tam giác BCD,ACD,ABD,AB
ii) \(\frac{GA}{GG_A}=\frac{GB}{GG_B}=\frac{GC}{GG_C}=\frac{GD}{GG_D}=3\)
iii) \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
2) Ta phát biểu bổ đề sau: Cho tam giác ABC, điểm M thuộc đường thẳng BC. Ta có \(\overrightarrow{AM}=\frac{\overline{BM}}{\overline{BC}}\overrightarrow{AC}+\frac{\overline{CM}}{\overline{CB}}\overrightarrow{AB}\)
A B C M N
Chứng minh: Lấy điểm N trên AB sao cho MN || AC, ta có:
\(\overrightarrow{AM}=\overrightarrow{AN}+\overrightarrow{NM}=\frac{\overline{AN}}{\overline{AB}}\overrightarrow{AB}+\frac{\overline{NM}}{\overline{AC}}\overrightarrow{AC}=\frac{\overline{CM}}{\overline{CB}}\overrightarrow{AB}+\frac{\overline{BM}}{\overline{BC}}\overrightarrow{AC}\)
Lời giải:
A B C D A' B' C' D' G A G
Gọi G và G' lần lượt là trọng tâm của tứ diện ABCD và A'B'C'D'.
Ta có: \(\overrightarrow{AG}=\frac{3}{4}\overrightarrow{AG_A}=\frac{3}{4}.\frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}}{4}\left(1\right)\)
Mặt khác \(\frac{\overline{A'A}}{\overline{A'B}}=\frac{\overline{B'B}}{\overline{B'C}}=\frac{\overline{C'C}}{\overline{C'D}}=\frac{\overline{D'D}}{\overline{D'A}}=k\), suy ra:
\(\frac{\overline{AA'}}{\overline{AB}}=\frac{\overline{BB'}}{\overline{BC}}=\frac{\overline{CC'}}{\overline{CD}}=\frac{k}{k-1};\frac{\overline{AD'}}{\overline{AD}}=\frac{\overline{DC'}}{\overline{DC}}=\frac{\overline{CB'}}{\overline{CB}}=\frac{-1}{k-1}\)
Từ đó: \(\overrightarrow{AA'}=\frac{\overline{AA'}}{\overline{AB}}\overrightarrow{AB}=\frac{k}{k-1}\overrightarrow{AB};\overrightarrow{AD'}=\frac{-1}{k-1}\overrightarrow{AD}\)
\(\overrightarrow{AB'}=\frac{\overline{BB'}}{\overline{BC}}\overrightarrow{AC}+\frac{\overline{CB'}}{\overline{CB}}\overrightarrow{AB}=\frac{k}{k-1}\overrightarrow{AC}-\frac{1}{k-1}\overrightarrow{AB}\)
\(\overrightarrow{AC'}=\frac{\overline{CC'}}{\overline{CD}}\overrightarrow{AD}+\frac{\overline{DC'}}{\overline{DC}}\overrightarrow{AC}=\frac{k}{k-1}\overrightarrow{AD}-\frac{1}{k-1}\overrightarrow{AC}\)
Suy ra \(\overrightarrow{AG'}=\frac{1}{4}\left(\overrightarrow{AA'}+\overrightarrow{AB'}+\overrightarrow{AC'}+\overrightarrow{AD'}+\overrightarrow{A'G'}+\overrightarrow{B'G'}+\overrightarrow{C'G'}+\overrightarrow{D'G'}\right)\)
\(=\frac{\overrightarrow{AA'}+\overrightarrow{AB'}+\overrightarrow{AC'}+\overrightarrow{AD'}}{4}\)
\(=\frac{1}{4}\left(\frac{k}{k-1}\overrightarrow{AB}+\frac{k}{k-1}\overrightarrow{AC}-\frac{1}{k-1}\overrightarrow{AB}+\frac{k}{k-1}\overrightarrow{AD}-\frac{1}{k-1}\overrightarrow{AC}-\frac{1}{k-1}\overrightarrow{AD}\right)\)
\(=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}}{4}\left(2\right)\)
Từ (1),(2) suy ra \(\overrightarrow{AG}=\overrightarrow{AG'}\). Vậy G trùng G' hay hai tứ diện ABCD và A'B'C'D' có cùng trọng tâm.

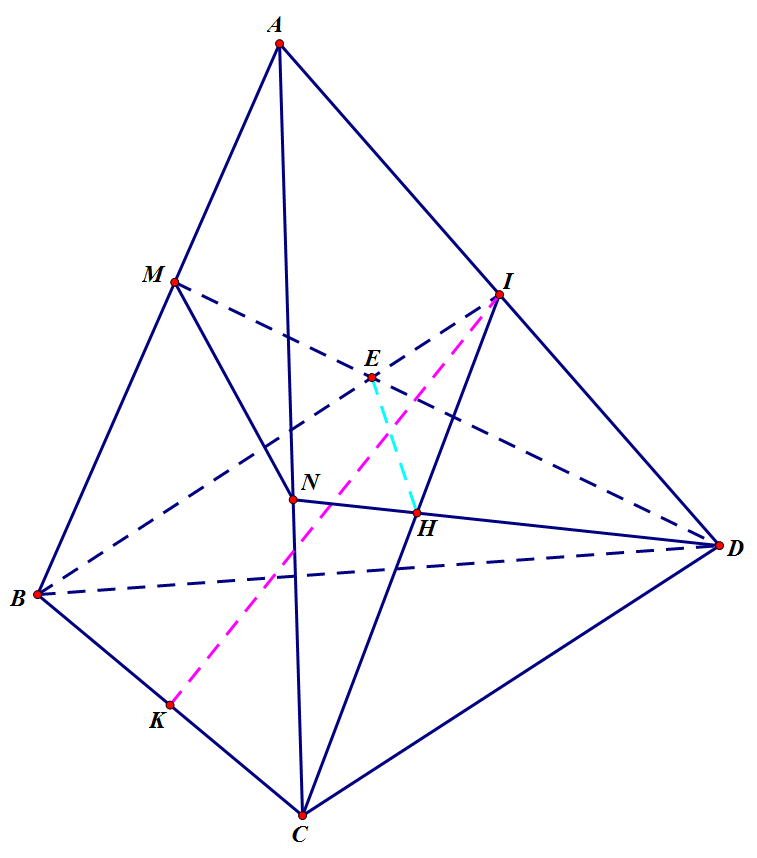
a,Hiển nhiên : K ∈ (KAD), mà K ∈ BC nên K ∈ (BCD)
Hiển nhiên : D ∈ (KAD) và D ∈ (BCD)
⇒ (KAD) \(\cap\) (BCD) = DK
b, Hiển nhiên : K ∈ (KAD), mà K ∈ BC nên K ∈ (IBC)
Hiển nhiên I ∈ (IBC), mà I ∈ AD nên I ∈ (KAD)
⇒ (KAD) \(\cap\) (BCI) = IK
c, Trong (ABD) gọi E là giao điểm của BI và DM
⇒ \(\left\{{}\begin{matrix}E\in\left(IBC\right)\\E\in\left(DMN\right)\end{matrix}\right.\)
Trong (ACD) gọi F là giao điểm của CI và DN
⇒ \(\left\{{}\begin{matrix}F\in\left(IBC\right)\\F\in\left(DMN\right)\end{matrix}\right.\)
Vậy (DMN) \(\cap\) (IBC) = EF

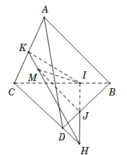
Trong mặt phẳng (BCD); IJ cắt CD tại H nên H thuộc (ACD)
Điểm H thuộc IJ m suy ra bốn điểm M; I; J; H đồng phẳng.
Nên trong mặt phẳng (IJM) , MH cắt IJ tại H và M H ⊂ I J M .
Mặt khác M ∈ A C D H ∈ A C D ⇒ M H ⊂ A C D .
Vậy giao tuyến của 2 mặt phẳng (ACD) và ( IJM) là MH
Chọn D.

Trong mp(BCD), gọi M là giao điểm của KJ với DC
\(M\in KJ\subset\left(IJK\right)\)
\(M\in CD\subset\left(ACD\right)\)
Do đó: \(M\in\left(IJK\right)\cap\left(ACD\right)\left(1\right)\)
\(I\in AC\subset\left(ACD\right);I\in\left(IJK\right)\)
=>\(I\in\left(ACD\right)\cap\left(IJK\right)\left(2\right)\)
Từ (1) và (2) suy ra \(\left(IJK\right)\cap\left(ACD\right)=MI\)
Xét ΔCAB có
\(\dfrac{CI}{CA}=\dfrac{CJ}{CB}=\dfrac{1}{2}\)
nên IJ//AB
\(K\in BD\subset\left(ABD\right);K\in\left(IJK\right)\)
=>\(K\in\left(ABD\right)\cap\left(IJK\right)\)
Xét (ABD) và (IJK) có
\(K\in\left(ABD\right)\cap\left(IJK\right)\)
IJ//AB
Do đó: (ABD) giao (IJK)=xy, xy đi qua K và xy//IJ//AB

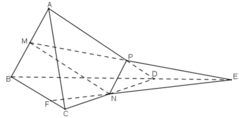
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.