Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

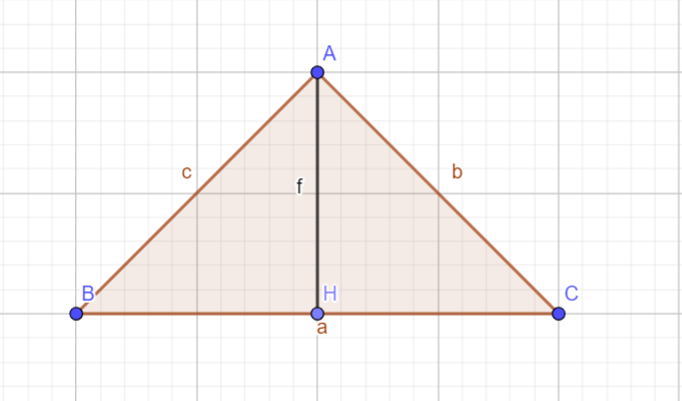
a) Xét tam giác AHB và AHC có:
AC = BC (gt)
\(\widehat{AHB}=\widehat{AHC}\) (AH vuông góc BC)
=> AHB = AHC (ch-gv)
=> HB = HC (cạnh tương ứng)
\(\widehat{BAH}=\widehat{CAH}\) (góc tương ứng)
b) Ta có HB = HC (cmt)
Mặt khác AH là cạnh góc vuông của tam giác vuông AHC
Áp dụng định lý Pitago ta có:
\(AC^2=AH^2+HC^2\\ =>10^2=AH^2+6^2\\ =>100=AH^2+36\)
\(=>AH^2=100-36=64\\ =>AH=\sqrt{64}=8\)

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H

:
a)Vì △ABC cân tại A nên AH là đg cao đồng thời cx là đg p/g, đường trung tuyến.
HB=HC và BAHˆ=CAHˆ
b)HC=BC2=82=4
Áp dụng định lý Py-ta-go vào tam gíác vuông AHC có:
AH2=AC2−HC2=.......
AH=...........
c)Xét 2 tam gíác vuông : BDH và CEH có
HB=HC(cmt)
Bˆ=Cˆ(△ABC cân)
Do đó: △BDH=△CEH
DH =EH
dpcm
Bài 3 :
a)Vì △ABC cân tại A nên AH là đg cao đồng thời cx là đg p/g, đường trung tuyến.
HB=HC và BAHˆ=CAHˆ
b)HC=BC2=82=4
Áp dụng định lý Py-ta-go vào tam gíác vuông AHC có:
AH2=AC2−HC2=.......
AH=...........
c)Xét 2 tam gíác vuông : BDH và CEH có
HB=HC(cmt)
Bˆ=Cˆ(△ABC cân)
Do đó: △BDH=△CEH
DH =EH
dpcm

a/ Xét tam giác ABH( góc H = 90 độ) và tam giác ACH( góc H = 90 độ)
Có: AB=AC(gt)
Góc ABH = góc ACH(gt)
=> Tam giác ABH = tam giác ACH (cạnh huyền - góc nhọn)
=>HB=HC (2 cạnh tương ứng)
=>Góc CAH = góc BAH( 2 góc tương ứng)
b/ Ta có :HB=HC( cmt)
=> H trung điểm BC
Ta có: HB=HC=BC/2=8/2=4 (cm)
Xét tam giác ABH vuông tại H
Có AB^2= AH^2+HB^2 (pytago)
=>AH^2= AB^2-HB^2
AH^2= 5^2-4^2
AH^2=25-16
AH^2=9
AH= căng 9
=> AH= 3cm
Vậy AH=3cm
c/ Xét tam giác ADH( góc D=90 độ) và tam giác AEH ( góc E = 90 độ)
Có: AH chung
Góc DAH= góc EAH ( tam giác ABH= tam giác ACH)
=> tam giác ADH= tam giác AEH ( cạnh huyền - góc nhọn)
=> AD=AE ( 2 cạnh tương ứng)
=> Tam giác ADE cân tại A ( 2 cạnh bên bằng nhau)
Xét tam giác ABC cân tại A(gt)
Có: Góc B= (180 độ - góc A)/2 (định lí)
Xét tam giác ADE cân tại A (cmt)
Có: Góc D= (180 độ - góc A)/2 (định lí)
=> Góc B= Góc D ( =(180 độ - góc A)/2)
=> DE//BC ( 2 góc đồng vị bằng nhau)

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng) và \(\widehat{BAH}=\widehat{CAH}\)(Hai góc tương ứng)

A B C D E H
a, Xét \(\Delta ABH\) và\(\Delta ACH\) CÓ:
\(AHchung\)
AB = AC
\(\widehat{AHB}=\widehat{AHC}\)
\(\Rightarrow\Delta ABH=\Delta ACH\)(cạnh huyền cạnh góc vuông)
=> BH = HC ( 2 cạnh tương ứng )
b,Do BC = 8cm => BH = 4cm
Áp dụng định lý Py ta go vào tam giác vuông ABH có :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH^2=AB^2-BH^2\)\(\Rightarrow AH^2=5^2-4^2=25-16=9\)\(\Rightarrow AH=3\left(cm\right)\)
c,\(Xét\Delta DBH\) và\(\Delta ECH\) có :
\(\widehat{ABH}=\widehat{ACH}\)
BH = HC
\(\widehat{BDH}=\widehat{CEH}\)
\(\Rightarrow\Delta DBH=\Delta ECH\)\(\Rightarrow DH=EH\)=> \(\Delta DHE\) cân tại H
cho mình 1 tym nha

a)Chứng minh được tam giác ABH= tam giác ACH( ch-cgv)
Suy ra: HB=HC(yttư)(đpcm). Vậy H là trung điểm BC.Suy ra HB=HC=BC:2=8:2=4
và góc BAH=góc CAH(yttư)(đpcm)
b) Ta có: tam giác ABH vuông tại H(AH vuông góc BC)
Suy ra AH^2 + BH^2 =AB^2
Suy ra AH^2+4^2= 5^2
Suy ra AH^2= 9
Mà AH>0
Suy ra AH=3
c) Xét tam giác ADH và tam giác AEH, ta có:
Góc ADH= Góc AEH=90 ĐỘ ( HD vuông góc AB, HE vuông góc AC)
AH là cạnh chung
Góc DAH= Góc EAH(yttư do tam giác ABH= tam giác ACH)
Suy ra tam giác ADH= tam giác AEH(ch-gh)
Suy ra HD=HE(yttư)
Suy ra tam giác HDE cân tại H(đpcm)

tu ve hinh :
AB = AC => tamgiac ABC can tai A (dn)
xet tamgiac AHB va tamgiac AHC co :
AB = AC va goc ABC = gocACB do tamgiac ABC can tai A (cmt)
goc AHB = goc AHC = 90 do AH | BC (gt)
=> tamgiac AHB = tamgiac AHC (ch - gn)
=> HB = HC (dn)
b, cau nay de tu ap dung PY-TA-GO ma lam
c,
+ xet tamgiac DHB va tamgiac EHC co :
goc ABC = goc ACB (cau a)
BH = HC (cau a)
goc BDH = goc HEC = 90 do HD | AB va HE | AC (gt)
=> tamgiac DHB = tamgiac EHC(ch - gn)
=> DH = DE (dn)
=> tamgiac DHE can tai H (dn)
+ co AD + DB = AB
AE + EC = AC
AB = AC (cau a)
BD = EC do tamgiac HDB = tamgiac HEC (cau b)
=> DA = AE
DE cat AH tai O
xet tamgiac DAO va tamgiac EAO co : AO chung
goc BAH = goc CAH do tamgiac AHB = tamgiac AHC (cau a)
=> tamgiac DAO = tamgiac EAO (c - g - c)
=> AD = AE (dn)
=> tamgiac ADE can tai A (dn)
=> goc ADE = (180 - goc BAC) : 2 (tc)
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc ADE = goc ABC ma 2 goc nay dong vi
=> DE//BC (tc)
- tự vẽ hình
a)Xét 2 tam giác vuông ABH và ACH, ta có:
AB=AC(tam giác ABC cân tại A)
Góc ABH = góc ACH(tam giác ABC cân tại A)
Vậy tam giác vuông ABH = tam giác vuông ACH
=> HB=HC(cặp cạnh t/ứng)
và góc BAH = góc CAH (cặp góc t/ứng)
b) Ta có HB=HC(cmt)
mà HB+HC=8 (cm) => HB=HC=4(cm)
Áp dụng định lý pytago vào tam giác vuông AHB, ta có:
AH2+BH2=AB2
=> AH2=AB2-BH2=25-16=9 => AH=3
c) Xét tam giác vuông BDH và tam giác vuông CEH, ta có:
BH=HC(cmt)
góc DBH=góc ECH(tam giác ABC cân tại A)
Vậy tam giác vuông BDH = tam giác vuông CEH
=> DH=EH(cặp cạnh t/ứng)
=> tam giác HDE là tam giác cân tại H
d) c/m DE//BC( ko có câu d nhưng vt cho dễ nhìn)
Góc BHD=Góc CHE(tam giác vuông BDH = tam giác vuông CEH)
Ta có: Góc BHD + góc CHE+ góc DHE=180 độ
-Góc HDE+Góc DEH+ Góc DHE-180 độ(tổng 3 góc của 1 tam giác)
Mà Góc BHD=Góc CHE và Góc HDE=Góc DEH(tam giác HDE cân tại H)
=> Góc BHD=Góc CHE = Góc HDE=Góc DEH
Mà hai góc DEH và CHE ở vị trí so le trong
=> DE//BC
`Answer:`
a. Xét `\triangleABH` và `\triangleACH:`
`AH` chung
`AB=AC`
`\hat{AHB}=\hat{AHC}=90^o`
`=>\triangleABH=\triangleACH(ch-cgv)`
`=>HB=HC`
`=>\hat{HAB}=\hat{HAC}`
b. Ta có: \(HB=HC=\frac{BC}{2}=\frac{12}{2}=6cm\)
Áp dụng định lý Pytago vào tam giác `AHB` vuông tại H:
\(AH^2+HB^2=AB^2\Leftrightarrow AH^2+6^2=10^2\Leftrightarrow AH^2+36=100\Leftrightarrow AH^2=64\Leftrightarrow AH=8cm\)