Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm

Ta có các điểm cực trị của (C) là A(0;4); B(2;0)
Gọi M (x;y) thuộc (P) : \(y=x^2\) khi đó \(\overrightarrow{MA}=\left(x;x^2-4\right);\overrightarrow{MB}=\left(x-2;\right)x^2\)
Tam giác AMB vuông tại M \(\Leftrightarrow\overrightarrow{AM}.\overrightarrow{BM}=0\Leftrightarrow x\left(x-2\right)+x^2\left(x^2-4\right)=0\)
\(\Leftrightarrow x\left(x^3-3x-2\right)=0\)
\(\Leftrightarrow x\left(x+1\right)^2\left(x-2\right)=0\)
Vậy có 3 điểm M thuộc (P) để tam giác AMB vuông tại M là \(M_1\left(0;0\right);M_2\left(-1;1\right);M_3\left(2;4\right)\)

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

- Ta có \(y'=4x^3-4m^2x;y'=0\) \(\Leftrightarrow\begin{cases}x=0\\x^2=m^2\end{cases}\) Điều kiện có 3 điểm cực trị : \(m\ne0\)
- Tọa độ 3 điểm cực trị : A (0;1); B \(\left(-m;1-m^4\right),C\left(m;1-m^4\right)\)
- Chứng minh tam giác ABC cân đỉnh A. Tọa độ trung điểm I của BC là I \(\left(0;1-m^4\right)\)
- \(S_{ABC}=\frac{1}{2}AI.BC=m^4\left|m\right|=\left|m\right|^5=32\Leftrightarrow m=\pm2\left(tm\right)\)

- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
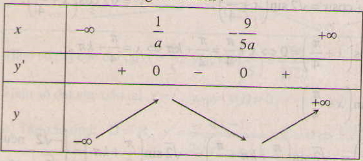
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
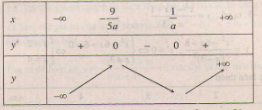
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.

Ta có : \(y'=3x^2+6x=0\Leftrightarrow\begin{cases}x=-2\Rightarrow y=m+4\\x=0\Rightarrow y=m\end{cases}\)
Vậy hàm số có 2 điểm cực trị \(A\left(0;m\right);B\left(-2;m+4\right)\)
Ta có \(\overline{OA}=\left(O;m\right);\overline{OB}=\left(-2;m+4\right)\)
Để \(\widehat{AOB}=120^0\) thì \(\cos AOB=-\frac{1}{2}\)
\(\Leftrightarrow\frac{m\left(m+4\right)}{\sqrt{m^2\left(4+\left(m+4\right)^2\right)}}=-\frac{1}{2}\)
\(\Leftrightarrow\) \(m=\frac{-12\pm2\sqrt{3}}{3}\) và -4<m<0
\(\Leftrightarrow m=\frac{-12\pm2\sqrt{3}}{3}\)