Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(2^{x+1}.\left(-3\right)^y=12^x\)
\(\Rightarrow2^{x+1}.\left(-3\right)^y=\left(3.4\right)^x\)
\(\Rightarrow2^{x+1}.\left(-3\right)^y=3^x.4^x\)
\(\Rightarrow2^{x+1}.\left(-3\right)^y=3^x.2^{2x}\)
\(\Rightarrow2^{x+1}.\left(-1\right)^y.3^y=3^x.2^{2x}\)
\(\Rightarrow\left[{}\begin{matrix}x+1=2x\\x=y\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=y=1\end{matrix}\right.\)
Vậy x=1 , y=1

Đáp án C
Đặt t = y x > 1 ⇒ y = t x ⇒ P = log x t x 2 - 1 2 + 8 log t t x x 2
= log x t 2 + 1 2 + 8 log t t x - log t x 2 = 2 log x t 2 + 1 2 + 8 1 + log t x - 1 2 log t x 2
Đặt u = log t x ⇒ P = 2 u + 1 2 + 8 1 + 1 2 u 2 = 4 u 2 + 4 u + 2 u 2 + 8 u + 9 = P u
Do u = log x y x = log x y - 1 > 0 nên xét P u u > 0 ⇒ P ' u = 8 u + 4 - 4 u 3 - 8 u 2
= 4 2 u + 1 u 3 - 1 u 3 = 0 → u > 0 u = 1 . Do đó ta tìm được P m i n = P 1 = 27 .

Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8 , xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0 .
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5 và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5 .
Do đó 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 ⇔ [ x = - 1 x = 3 y = - 3 ⇒ x ; y = - 1 ; - 3 ; 3 ; - 3 .
Vậy có tất cả hai cặp số thực (x;y) thỏa mãn yêu cầu bài toán.

Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .

Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)
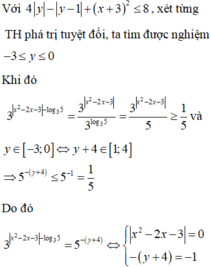



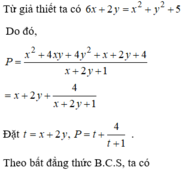
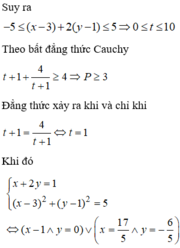
Đáp án B
Ta có 3 x - y + 5 x y i = x 2 - y 2 + 2 x y i ⇔ 5 x y - y = 2 x y 3 x = x 2 - y 2 ⇒ [ y = 0 x = 1 3 ⇒ y 2 = - 8 9 .