
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

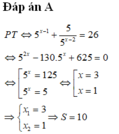

14.
\(log_aa^2b^4=log_aa^2+log_ab^4=2+4log_ab=2+4p\)
15.
\(\frac{1}{2}log_ab+\frac{1}{2}log_ba=1\)
\(\Leftrightarrow log_ab+\frac{1}{log_ab}=2\)
\(\Leftrightarrow log_a^2b-2log_ab+1=0\)
\(\Leftrightarrow\left(log_ab-1\right)^2=0\)
\(\Rightarrow log_ab=1\Rightarrow a=b\)
16.
\(2^a=3\Rightarrow log_32^a=1\Rightarrow log_32=\frac{1}{a}\)
\(log_3\sqrt[3]{16}=log_32^{\frac{4}{3}}=\frac{4}{3}log_32=\frac{4}{3a}\)
11.
\(\Leftrightarrow1>\left(2+\sqrt{3}\right)^x\left(2+\sqrt{3}\right)^{x+2}\)
\(\Leftrightarrow\left(2+\sqrt{3}\right)^{2x+2}< 1\)
\(\Leftrightarrow2x+2< 0\Rightarrow x< -1\)
\(\Rightarrow\) có \(-2+2020+1=2019\) nghiệm
12.
\(\Leftrightarrow\left\{{}\begin{matrix}x-2>0\\0< log_3\left(x-2\right)< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>2\\1< x-2< 3\end{matrix}\right.\)
\(\Rightarrow3< x< 5\Rightarrow b-a=2\)
13.
\(4^x=t>0\Rightarrow t^2-5t+4\ge0\)
\(\Rightarrow\left[{}\begin{matrix}t\le1\\t\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}4^x\le1\\4^x\ge4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\le0\\x\ge1\end{matrix}\right.\)

Bài này cứ giải thẳng ra thôi có vấn đề gì đâu nhỉ?
\(f'\left(x\right)=3x^2+6x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=2\\x=-2\Rightarrow y=6\end{matrix}\right.\) \(\Rightarrow A\left(-2;6\right);B\left(0;2\right)\)
Hàm trùng phương thì dễ hơn, nếu thuộc lý thuyết ta nhận xét được ngay: do hệ số a=1>0 nên cực đại của hàm xảy ra tại \(x=0\Rightarrow y=-2\Rightarrow C\left(0;-2\right)\)
\(AB=2\sqrt{5};AC=2\sqrt{17};BC=4\) \(\Rightarrow S=4+2\sqrt{5}\)
Loại đáp án A và C, nhẩm được ngay trung điểm AC có tọa độ \(\left(-1;2\right)\) thay vào D thỏa mãn \(\Rightarrow D\) đúng
Hoặc cẩn thận hơn thì mất tầm 30s để viết pt trung trực cũng được

\(y'=x^2-\left(3m+2\right)x+2m^2+3m+1\)
\(\Delta=\left(3m+2\right)^2-4\left(2m^2+3m+1\right)=m^2\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\frac{3m+2+m}{2}=2m+1\\x_2=\frac{3m+2-m}{2}=m+1\end{matrix}\right.\)
Để hàm số có cực đại, cực tiểu \(\Rightarrow x_1\ne x_2\Rightarrow m\ne0\)
- Nếu \(m>0\Rightarrow2m+1>m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=m+1\\x_{CT}=2m+1\end{matrix}\right.\)
\(\Rightarrow3\left(m+1\right)^2=4\left(2m+1\right)\) \(\Rightarrow3m^2-2m-1=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-\frac{1}{3}< 0\left(l\right)\end{matrix}\right.\)
- Nếu \(m< 0\Rightarrow m+1>2m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=2m+1\\x_{CT}=m+1\end{matrix}\right.\)
\(\Rightarrow3\left(2m+1\right)^2=4\left(m+1\right)\Rightarrow12m^2+8m-1=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\frac{-2+\sqrt{7}}{6}>0\left(l\right)\\m=\frac{-2-\sqrt{7}}{6}\end{matrix}\right.\) \(\Rightarrow\sum m=\frac{4-\sqrt{7}}{6}\)

Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
- Tập xác định : (-∞, 0)∪ (0, +∞)
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
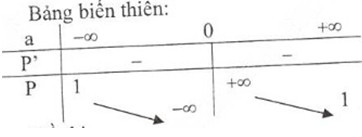
- Bảng biến thiên:
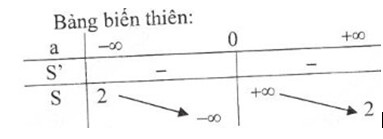
Đồ thị hàm số:
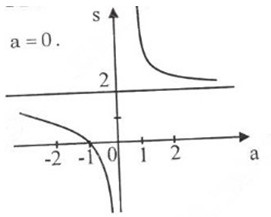
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
Đồ thị hàm số:
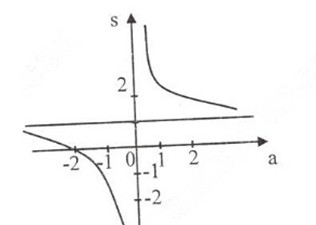
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.

Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A

18.
\(F\left(x\right)=\int\limits xe^{x^2}dx\)
Đặt \(t=x^2\Rightarrow xdx=\frac{1}{2}dt\)
\(\Rightarrow F\left(x\right)=\frac{1}{2}\int e^tdt=\frac{1}{2}e^t+C=\frac{1}{2}e^{x^2}+C\)
Ủa bạn có ghi nhầm đáp án A ko? Thế nào thì cả A và D đều ko phải nguyên hàm
19.
\(F\left(x\right)=\int sin^4xcosxdx=\int sin^4x.d\left(sinx\right)=\frac{1}{5}sin^5x+C\)
20.
Đặt \(4x=t\Rightarrow dx=\frac{1}{4}dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=2\Rightarrow t=8\end{matrix}\right.\)
\(\int\limits^2_0f\left(4x\right)dx=\int\limits^8_0\frac{1}{4}f\left(t\right)dt=\frac{1}{4}\int\limits^8_0f\left(x\right)dx=\frac{1}{4}.24=6\)
15.
\(t=cosx\Rightarrow sinx.dx=-dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=1\\x=\frac{\pi}{2}\Rightarrow t=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1e^t\left(-dt\right)=\int\limits^1_0e^tdt\)
Nếu cần kết quả tích phân thì \(I=e-1\)
16.
\(t=x^2\Rightarrow x.dx=\frac{1}{2}dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=2\Rightarrow t=4\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^4_04^t\left(\frac{1}{2}dt\right)=\frac{1}{2}\int\limits^4_04^tdt\)
17.
\(t=x^2+2x\Rightarrow\left(x+1\right)dx=\frac{1}{2}dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=1\Rightarrow t=3\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^3_0e^t\left(\frac{1}{2}dt\right)=\frac{1}{2}\int\limits^3_0e^tdt\)

14.
\(d\left(I;\left(P\right)\right)=\frac{\left|1-2.2+2-8\right|}{\sqrt{1^2+\left(-2\right)^2+\left(-2\right)^2}}=3\)
Áp dụng định lý Pitago:
\(R=\sqrt{4^2+d^2\left(I;\left(P\right)\right)}=\sqrt{4^2+3^2}=5\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2=25\)
15.
\(\overrightarrow{AB}=\left(2;1;-2\right)\) ; \(\overrightarrow{AC}=\left(-12;6;0\right)\)
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(12;24;24\right)=12\left(1;2;2\right)\)
\(\Rightarrow\) Mặt phẳng (ABC) nhận \(\left(1;2;2\right)\) là 1 vtpt
18.
\(D\in Ox\Rightarrow D\left(a;0;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AD}=\left(a-3;4;0\right)\\\overrightarrow{BC}=\left(4;0;-3\right)\end{matrix}\right.\)
\(AD=BC\Leftrightarrow\left(a-3\right)^2+4^2=4^2+\left(-3\right)^2\)
\(\Leftrightarrow\left(a-3\right)^2=9\Rightarrow\left[{}\begin{matrix}a=0\\a=6\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}D\left(0;0;0\right)\\D\left(6;0;0\right)\end{matrix}\right.\)
11.
Mặt cầu (S) tâm \(I\left(1;-2;0\right)\) bán kính \(R=\sqrt{1^2+\left(-2\right)^2-\left(-4\right)}=3\)
\(d\left(I;\left(P\right)\right)=\frac{\left|1-2-0+4\right|}{\sqrt{1^2+1^2+\left(-1\right)^2}}=\sqrt{3}\)
Gọi bán kính đường tròn (C) là \(r\)
Áp dụng định lý Pitago:
\(r=\sqrt{R^2-d^2\left(I;\left(P\right)\right)}=\sqrt{6}\)
Diện tích đường tròn: \(S=\pi r^2=6\pi\)