Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Xét hàm số 
trên đoạn 
Ta có 
; 
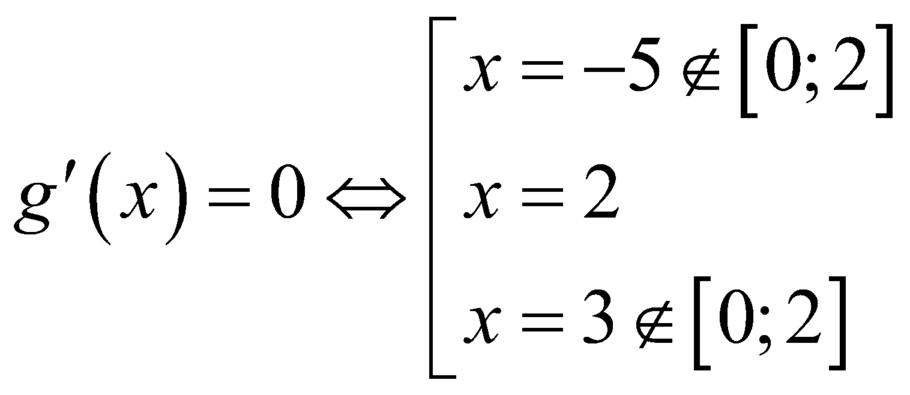
Bảng biến thiên
; 
.
Để 
thì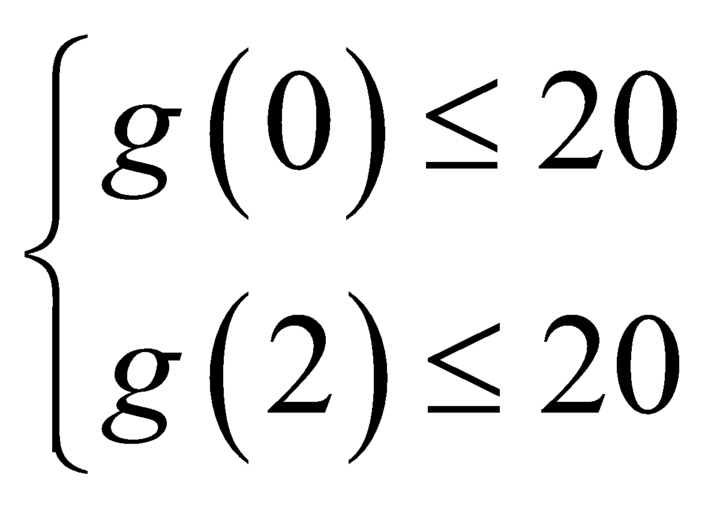 
.
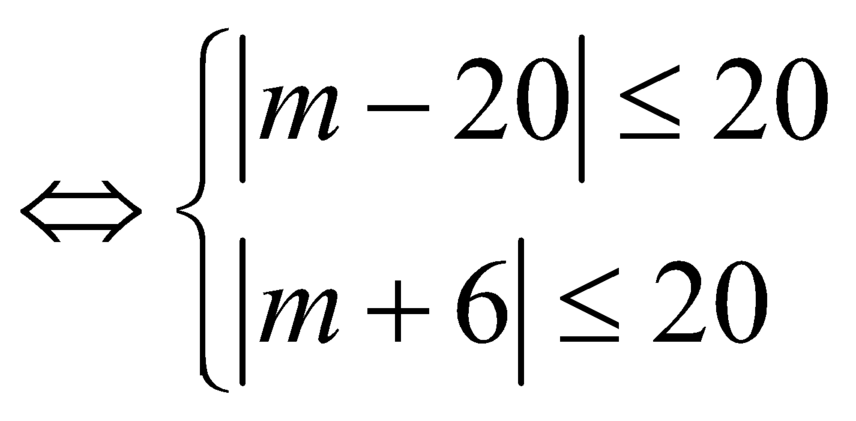
Mà 
nên 
.
Vậy tổng các phần tử của 
là 
.
Chọn C
Xét hàm số 
trên đoạn [0;2]
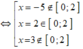
Bảng biến thiên:
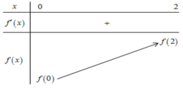
với f(0) = m - 20; f(2) = m + 6
Xét hàm số y = 1 4 x 4 - 19 2 x 2 + 30 x + m - 20 trên đoạn [0;2]
+ Trường hợp 1: 
Ta có:
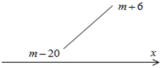
suy ra không có giá trị m.
+ Trường hợp 2: 
Ta có:
Vì m nguyên nên 
+ Trường hợp 3: 
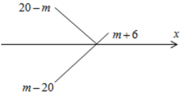
Vì m nguyên nên 
Vậy 
Tổng các phần tử của S bằng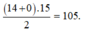 
\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.
Xét
\(y'=4x^3-4\left(m-1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=m-1\end{cases}}\)
TH1:
\(m-1\le0\) thì hàm số đồng biến trên R
TH2: \(m-1>0\Rightarrow\orbr{\begin{cases}x=\sqrt{m-1}\\x=-\sqrt{m-1}\end{cases}}\)
Khi đó khoảng đồng biến của hàm số là \(\left(-\infty,-\sqrt{m-1}\right)\text{ và }\left(0,\sqrt{m-1}\right)\)
Muốn hàm số đồng biến trên (1,3) thì \(\left(1,3\right)\subset\left(0,\sqrt{m-1}\right)\Leftrightarrow3\le\sqrt{m-1}\Leftrightarrow m\ge10\)
Vậy \(\orbr{\begin{cases}m\le1\\m\ge10\end{cases}}\)
\(f\left(x\right)=x^4-6mx^2+m^2\Rightarrow f'\left(x\right)=4x^3-12mx\)
\(f'\left(x\right)=0\Leftrightarrow4x\left(x^2-3m\right)=0\)
- Nếu \(m\le0\Rightarrow\) hàm đạt GTLN tại \(x=-2\)
\(f\left(-2\right)=m^2-24m+16=16\Rightarrow\left[{}\begin{matrix}m=0\\m=24\left(ktm\right)\end{matrix}\right.\)
- Nếu \(m>0\) hàm có 3 cực trị: \(x=0\) là cực đại, \(x=\pm\sqrt{3m}\) là 1 cực tiểu
TH1: \(m\ge\frac{4}{3}\Rightarrow-\sqrt{3m}\le-2< 1< \sqrt{3m}\)
\(\Rightarrow f\left(x\right)_{max}=f\left(0\right)=m^2=16\Rightarrow m=4\) (thỏa mãn)
- Nếu \(0< m< \frac{4}{3}\)
\(\Rightarrow f\left(x\right)_{max}=max\left\{f\left(0\right);f\left(-2\right)\right\}=max\left\{m^2;m^2-24m+16\right\}\)
+ Với \(m< \frac{2}{3}\Rightarrow f\left(x\right)_{max}=f\left(-2\right)=m^2-24m+16=16\)
\(\Rightarrow\left[{}\begin{matrix}m=0\\m=24\end{matrix}\right.\) (ktm)
- Với \(\frac{2}{3}\le m< \frac{4}{3}\Rightarrow f\left(x\right)_{max}=f\left(0\right)=m^2< \frac{16}{9}< 16\left(ktm\right)\)
Vậy \(S=\left\{0;4\right\}\)
Cho e hỏi đoạn nếu 0<m<4/3 sao suy ra được f max chỉ có thể là f(0) hoặc f(-2) ạ? Còn f(1) thì sao ạ? Em cảm ơn ạ
Bạn coi lại đề, GTLN của hàm số trên đoạn \(\left[-1;2\right]\) khi \(x=-1\) bằng 5 là sao nhỉ?
Phương trình hoành độ giao điểm : \(-x^4+2\left(2+m\right)x^2-3-2m=0\left(1\right)\)
Đặt \(t=x^2,\left(t\ge0\right)\), phương trình (1) trở thành : \(t^2-1\left(m+2\right)t+3+2m=0\left(2\right)\)
(1) có 4 nghiệm phân biệt khi và chỉ khi (2) có 2 nghiệm dương phân biệt
Điều kiện là : \(\begin{cases}\Delta'>0\\S>0\\P>0\end{cases}\) \(\Leftrightarrow\begin{cases}m^2+2m+1>0\\m+2>0\\3+2>0\end{cases}\) \(\Leftrightarrow\begin{cases}m\ne-1\\m>-\frac{3}{2}\end{cases}\) (*)
Với điều kiện (*), giả sử \(t_1;t_2\) (\(0 < t 1 < t2 \) là 2 nghiệm phân biệt của (2), khi đó (1) có 4 nghiệm phân biệt là \(x_1=-\sqrt{t_2};x_2=-\sqrt{t_1};x_3=\sqrt{t_1};x_4=\sqrt{t_2};\)
\(x_1;x_2;x_3;x_4\) lập thành một cấp số cộng khi và chỉ khi :
\(x_2-x_1=x_3-x_2=x_4-x_3\)
\(\Leftrightarrow t_2=9t_1\left(a\right)\)
Áp dụng định lí Viet ta có : \(t_1+t_2=2\left(m+2\right);t_1.t_2=3+2m\left(b\right)\)
Từ (a) và (b) ta có : \(9m^2-14m-39=0\)
Đối chiếu điều kiện (*) ta có \(m=3\) hoặc \(m=-\frac{13}{9}\)
\(f\left(x\right)=\dfrac{2x-1}{x-3}=\dfrac{2\left(x-3\right)+5}{x-3}=1+\dfrac{5}{\left(x-3\right)}\)
f(x) có dạng \(y=\dfrac{5}{x}\Rightarrow\) f(x) luôn nghịch biến
Tất nhiên bạn có thể tính đạo hàm --> f(x) <0 mọi x khác -3
f(x) luôn nghich biến [0;2] < -3 thuộc nhánh Bên Phải tiệm cận đứng
\(\Rightarrow\left\{{}\begin{matrix}Max=f\left(0\right)=\dfrac{1}{3}\\Min=f\left(2\right)=-3\end{matrix}\right.\)
Xét hàm \(f\left(x\right)=\frac{1}{4}x^4-14x^2+48x+m-30\)
\(f'\left(x\right)=x^3-28x+48=\left(2-x\right)\left(4-x\right)\left(x+6\right)\ge0\) ; \(\forall x\in\left[0;2\right]\)
\(\Rightarrow y=\left|f\left(x\right)\right|\) đạt max tại 1 trong 2 đầu mút
\(y\left(0\right)=\left|m-30\right|\) ; \(y\left(2\right)=\left|m+14\right|\)
TH1: \(m\ge30\Rightarrow y_{max}=y\left(2\right)=\left|m+14\right|=m+14\le30\)
\(\Rightarrow m\le16\) (ktm do \(m\ge30\))
TH2: \(m\le-14\Rightarrow y_{max}=\left|m-30\right|=30-m\le30\)
\(\Rightarrow m\ge0\) (ko thỏa mãn)
TH3: \(-14< m< 30\Rightarrow\left\{{}\begin{matrix}y\left(0\right)=30-m\\y\left(2\right)=m+14\end{matrix}\right.\)
- Nếu \(y_{max}=y\left(0\right)\Leftrightarrow\left\{{}\begin{matrix}30-m\ge m+14\\30-m\le30\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le8\\m\ge0\end{matrix}\right.\) \(\Rightarrow0\le m\le8\)
- Nếu \(y_{max}=y\left(2\right)\Rightarrow\left\{{}\begin{matrix}m+14\ge30-m\\m+14\le30\end{matrix}\right.\) \(\Rightarrow8\le m\le16\)
Vậy \(0\le m\le16\)