Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
Lê Huy Hoàng:
a) ĐK: $x\in\mathbb{R}\setminus \left\{k\pi\right\}$ với $k$ nguyên
PT $\Leftrightarrow \tan ^2x-4\tan x+5=0$
$\Leftrightarrow (\tan x-2)^2+1=0$
$\Leftrightarrow (\tan x-2)^2=-1< 0$ (vô lý)
Do đó pt vô nghiệm.
c)
ĐK:.............
PT $\Leftrightarrow 1+\frac{\sin ^2x}{\cos ^2x}-1+\tan x-\sqrt{3}(\tan x+1)=0$
$\Leftrightarrow \tan ^2x+\tan x-\sqrt{3}(\tan x+1)=0$
$\Leftrightarrow \tan ^2x+(1-\sqrt{3})\tan x-\sqrt{3}=0$
$\Rightarrow \tan x=\sqrt{3}$ hoặc $\tan x=-1$
$\Rightarrow x=\pi (k-\frac{1}{4})$ hoặc $x=\pi (k+\frac{1}{3})$ với $k$ nguyên
d)
ĐK:.......
PT $\Leftrightarrow \tan x-\frac{2}{\tan x}+1=0$
$\Leftrightarrow \tan ^2x+\tan x-2=0$
$\Leftrightarrow (\tan x-1)(\tan x+2)=0$
$\Rightarrow \tan x=1$ hoặc $\tan x=-2$
$\Rightarrow x=k\pi +\frac{\pi}{4}$ hoặc $x=k\pi +\tan ^{-2}(-2)$ với $k$ nguyên.
a) Trên hình là đô thị hàm số y = tanx , đường y = - 1 , y = 0 ( chính là trục x'Ox ) . ( thiếu hình vẽ )
Các điểm \(\left(-\frac{\pi}{4};-1\right);\left(\frac{3\pi}{4};-1\right)...\) là các điểm có hoành độ là nghiệm của phương trình tanx = - 1 . Các điểm \(\left(-\pi;0\right),\left(0;0\right),\left(\pi;0\right)\) , là các điểm có hoành độ là nghiệm của phương trình tanx = 0
b) Học sinh tự vẽ đô thị hàm số y = cotx và chỉ ra các điểm có hoành độ là nghiệm của phương cotx = \(\frac{\sqrt{3}}{3};cotx=1\)
a) \(x=-45^0+k90^0,k\in\mathbb{Z}\)
b) \(x=-\dfrac{\pi}{6}+k\pi,k\in\mathbb{Z}\)
c) \(x=\dfrac{3\pi}{4}+k2\pi,k\in\mathbb{Z}\)
d) \(x=300^0+k540^0,k\in\mathbb{Z}\)
a) Đặt t = cos
, t ∈ [-1 ; 1] thì phương trình trở thành
(1 - t2) - 2t + 2 = 0 ⇔ t2 + 2t -3 = 0 ⇔ 
Phương trình đã cho tương đương với
cos = 1 ⇔ = k2π ⇔ x = 4kπ, k ∈ Z.
b) Đặt t = sinx, t ∈ [-1 ; 1] thì phương trình trở thành
8(1 - t2) + 2t - 7 = 0 ⇔ 8t2 - 2t - 1 = 0 ⇔ t ∈ {
}.
Các nghiệm của phương trình đã cho là nghiệm của hai phương trình sau :
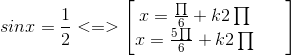
và 
Đáp số : x = 
+ k2π; x = 
+ k2π;
x = arcsin(
) + k2π; x = π - arcsin() + k2π, k ∈ Z.
c) Đặt t = tanx thì phương trình trở thành 2t2 + 3t + 1 = 0 ⇔ t ∈ {-1 ; 
}.
Vậy 
d) Đặt t = tanx thì phương trình trở thành
t - 
+ 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
Vậy 
Đáp án B
Phương pháp: Sử dụng công thức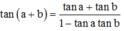
Cách giải:
Ứng với mỗi giá trị của k ta có 1 nghiệm x.
Vậy số phần tử của S là 20.