

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án B
Phương pháp
Chia các TH sau:
TH1: a<b<c.
TH2: a=b<c.
TH3: a<b=c.
TH4: a=b=c.
Cách giải
Gọi số tự nhiên có 3 chữ số là a b c ¯ (0≤a,b,c≤9, a≠0).
=> S có 9.10.10=900 phần tử. Chọn ngẫu nhiên một số từ S => n(Ω)=900
Gọi A là biến cố: “Số được chọn thỏa mãn a≤b≤c”.
TH1: a<b<c. Chọn 3 số trong 9 số từ 1 đến 9, có duy nhất một cách xếp chúng theo thứ tự tăng dần từ trái qua phải nên TH này có C 9 3 số thỏa mãn.
TH2: a=b<c, có C 9 2 số thỏa mãn.
TH3: a<b=c có C 9 2 số thỏa mãn.
TH4: a=b=c có 9 số thỏa mãn.
⇒ n ( A ) = C 9 3 + 2 C 9 2 + 9 = 165
Vậy P ( A ) = 11 60 .

Tập S có 9 4 phần tử. Ta có
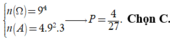
Thật vậy: Gọi số thỏa mãn biến cố là ![]()
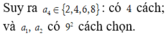
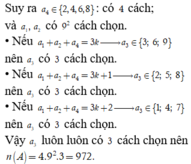

Đáp án A
Gọi số cần tìm có dạng a b c d ¯ vì a b c d ¯ chia hết cho 6 ⇒ d = { 2 ; 4 ; 6 ; 8 } a + b + c + d : 3 .
Khi đó, chọn d có 4 cách chọn; b và c đều có 9 cách chọn (từ 1 → 9 )
Nếu b + c + d:3 thì a = {3;6;9} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 1 thì a = {2;5;8} ⇒ có 3 cách chọn a
Nếu b + c + d chia 3 dư 2 thì a = {1;4;7} ⇒ có 3 cách chọn a
Suy ra a chỉ có 3 cách chọn ⇒ có 4.9.9.3 = 972 số chia hết cho 6
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .

Đáp án A.
Gọi số cần tìm có dạng
a
b
c
d
vì chia hết cho 6 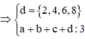
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1→9).
· Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
· Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
· Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là ![]()

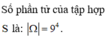
Gọi là biến cố: Chọn được 1 số chia hết cho 6 từ tập hợp S”
Số chia hết cho 6 có dạng: 


Gọi số tự nhiên có 4 chữ số khác nhau đôi một được chọn từ các chữ số 0; 1; 2; 3;4;5;6 là a b c d .
a có 6 cách chọn; các số còn lại có A 6 3 cách chọn. Suy ra số phần tử của S là 6 . A 6 3 = 720
Do đó n Ω = 720
Gọi A là biến cố: “số được chọn là số chẵn đồng thời chữ số hàng đơn vị bằng tổng các chữ số hàng chục, trăm và nghìn”.
Số được chọn thỏa mãn yêu cầu đề bài nếu
d ∈ 0 ; 2 ; 4 ; 6 d = a + b + c ⇒ d ∈ 4 ; 6 d = a + b + c .
* Trường hợp 1: Số có dạng a b c 4 với a + b + c = 4 suy ra tập { a;b;c } là { 0;1;3 }. Vì a,b,c đôi một khác nhau nên có 2 cách chọn a; 2 cách chọn b; 1 cách chọn c. Do đó số các số thuộc dạng này là 2 . 2 . 1 = 4
* Trường hợp 2: Số có dạng a b c 6 với a + b + c = 6 suy ra tập { a;b;c } có thể là một trong các tập { 0;1;5 }; { 0;2;4 }; { 1;2;3 }
+ Nếu { a;b;c } là tập { 0;1;5 } hoặc { 0;2;4 } thì mỗi trường hợp có 4 số (tương tự trường hợp trên)
+ Nếu { a;b;c } là tập { 1;2;3 } thì có P 3 = 3! = 6 số.
Do đó số các số thuộc dạng này là 4 + 4 + 6 = 14
Qua hai trường hợp trên, ta suy ra n(A): = 14 + 4 = 18.
Vậy xác suất cần tìm là
P A = n A n Ω = 18 720 = 1 40
Đáp án C