Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là điểm cách đều ba đỉnh của tam giác ABC
=> O là giao của 3 đường phân giác

Tham khảo:
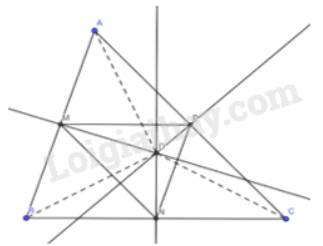
Theo giả thiết ta có :
OA = OB, MA = MB ( do M là trung điểm AB )
\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB
\( \Rightarrow \) MO vuông góc với AB
Theo giả thiết ta có :
OA = OC, PC = PA ( do P là trung điểm AC )
\( \Rightarrow \) PO là đường trung trực của đoạn thẳng AC
\( \Rightarrow \) PO vuông góc với AC
Theo giả thiết ta có :
OC = OB, NC = NB ( do N là trung điểm BC )
\( \Rightarrow \) NO là đường trung trực của đoạn thẳng BC
\( \Rightarrow \) NO vuông góc với BC

A B C M N O
a) xét tam giác vuông NCA và tam giác vuông MAC có
AC là cạnh huyền chung
góc A = góc C ( tam giác ABC cân tại B )
do đó tam giác NCA = tam giác MAC (cạnh huyền - góc nhọn )
suy ra NA = MC ( 2 cạnh tương ứng )
ta có BA = BC ( tam giác cân )
NA = MC (cmt)
suy ra BA-NA=BC-MC ( vì N nằm giữa B và A , M nằm giữa B và C )
hay BN = BM
xét \(\Delta BNO\)và \(\Delta BMO\)có
BO là cạnh huyền chung
BN = BM (cmt)
do đó \(\Delta BNO=\Delta BMO\)( cạnh huyền - cạnh góc vuông )
suy ra \(\widehat{NBO}=\widehat{MBO}\)( 2 góc tương ứng )
mà tia BO nằm giữa 2 tia BA và BC
suy ra tia Bo là phân giác góc ABC

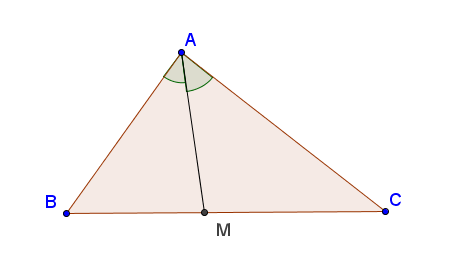
I là điểm cách đều ba cạnh nên AI là phân giác của góc BAC
O là điểm cách đều ba đỉnh nên OA=OB=OC
Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
=>ΔABO=ΔACO
=>góc BAO=góc CAO
=>AO là phân giác của góc BAC
=>A,I,O thẳng hàng

O là giao của ba đương phân giác
O cách đều 3 đỉnh tam giác ABC
=>OA=OB=OC
=> O là tâm đương tròn ngoại tiếp tam giác ABC