


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





A B C D M N Q P
a)
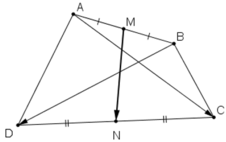
MN là đường trung bình của tam giác ABC nên \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AC}\).
QP là đường trung bình của tam giác ABC nên \(\overrightarrow{QP}=\dfrac{1}{2}\overrightarrow{AC}\).
Vậy \(\overrightarrow{MN}=\overrightarrow{QP}\).
b) Giả sử:
\(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}\Leftrightarrow\overrightarrow{MP}-\overrightarrow{MN}-\overrightarrow{MQ}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MP}+\overrightarrow{NM}+\overrightarrow{QM}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{QM}+\overrightarrow{MP}\right)+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{MN}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{QP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\) ( Điều giả sử đúng).
Vậy \(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}.\)

a)
A B C D M N P Q
Kẻ BD.
Trong tam giác ABD có MQ là đường trung bình nên MQ//BD và \(MQ=\dfrac{1}{2}BD\). (1)
Trong tam giác CBD có PN là đường trung bình nên PN//BD và \(NP=\dfrac{1}{2}BD\). (2)
Từ (1) và (2) suy ra: \(\overrightarrow{MQ}=\overrightarrow{NP}\).
Kẻ AC.
A B C D M N P Q
Trong tam giác ABC có MN là đường trung bình suy ra:
NM//CA và \(NM=\dfrac{1}{2}CA\). (3)
Trong tam giác DAC có PQ là đường trung bình nên:
PQ//AC và \(PQ=\dfrac{1}{2}CA\). (4)
Từ (3) và (4) suy ra: \(\overrightarrow{PQ}=\overrightarrow{NM}\).

1. Ta có MP là đường trung bình của tam giác ABD
=> MP // = 1/2 BD (1)
Ta có QN là đường trung bình của tam giác CBD
=> QN // = 1/2 BD (2)
(1) và (2) => đpcm
2. Ta có MQ là đường trung bình của tam giác ABC
=> MQ // = 1/2 AC (1)
Ta có PN là đường trung bình của tam giác ADC
=> PN // = 1/2 AC (2)
(1) và (2) => đpcm

Ta có : =
=
=
=> +
+
=
(
+
+
) =
=
=> +
+
=
(1)
Gọi G là trong tâm của tam giác MPR, ta có:
+
+
=
(2)
Mặt khác : =
+

A B C D I J
Áp dụng tính chất trung điểm ta có:
Do J là trung điểm của BD nên \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}\).
Theo quy tắc ba điểm: \(\overrightarrow{IB}=\overrightarrow{IA}+\overrightarrow{AB}\)
\(\overrightarrow{ID}=\overrightarrow{IC}+\overrightarrow{CD}\).
Vì vậy: \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}=\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{IC}+\overrightarrow{CD}\)
\(=\left(\overrightarrow{IA}+\overrightarrow{IC}\right)+\left(\overrightarrow{AB}+\overrightarrow{CD}\right)\)
\(=\overrightarrow{AB}+\overrightarrow{CD}\) (ĐPCM).