Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
heo me tim gtnn gtln cua bieu thuc:asinx + bcosx (a,b la hang so,a^2+b^2=/o)? | Yahoo Hỏi & Đáp
1.
ĐKXĐ: \(\left\{{}\begin{matrix}cos3x\ne0\\tan3x\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{6}+\frac{k\pi}{3}\\x\ne\frac{\pi}{12}+\frac{k\pi}{3}\end{matrix}\right.\)
2.
\(-1\le cos\frac{x}{2}\le1\Rightarrow\sqrt{2}\le\sqrt{cos\frac{x}{2}+3}\le2\)
\(\Rightarrow3\sqrt{2}-2\le y\le4\)
3.
a. \(\Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=sin3x\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{6}\right)=sin3x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=2x-\frac{\pi}{6}+k2\pi\\3x=\frac{7\pi}{6}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b. \(-4\left(1-cos^2x\right)+8\left(1-cosx\right)-1=0\)
\(\Leftrightarrow4cos^2x-8cosx+4=0\)
\(\Leftrightarrow cosx=1\)
\(\Leftrightarrow...\)
a: \(-1< =cosx< =1\)
\(\Leftrightarrow-2< =2cosx< =2\)
\(\Leftrightarrow-5< =2cosx-3< =-1\)
\(f\left(x\right)_{min}=-5\) khi cos x=-1
hay \(x=\Pi+k2\Pi\)
\(f\left(x\right)_{max}=-1\) khi cos x=1
hay \(x=k2\Pi\)
b: \(-1< =sinx< =1\)
\(\Leftrightarrow-2< =2sinx< =2\)
\(\Leftrightarrow5< =2sinx+7< =9\)
\(\Leftrightarrow\sqrt{5}< =\sqrt{2sinx+7}< =3\)
\(\Leftrightarrow3\sqrt{5}< =3\sqrt{2sinx+7}< =9\)
\(f\left(x\right)_{min}=3\sqrt{5}\) khi sin x=-1
hay \(x=-\dfrac{\Pi}{2}+k2\Pi\)
\(f\left(x\right)_{max}=9\) khi sin x=1
hay \(x=\dfrac{\Pi}{2}+k2\Pi\)
a) Do \(-1\le sinx\le1,\forall x\in R\).
Nên giá trị lớn nhất của \(y=3-4sinx\) bằng \(3-4.\left(-1\right)=7\)khi \(sinx=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{2}+k\pi\).
Giá trị nhỏ nhất của \(y=3-4sinx\) bằng \(3-4.1=-1\) đạt được khi \(sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\).
b) \(y=2-\sqrt{cosx}\) xác định khi \(0\le cosx\le1\) .
Giá trị lớn nhất của \(y=2-\sqrt{cosx}=2-\sqrt{0}=2\) khi \(cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\).
Giá trị nhỏ nhất của \(y=2-\sqrt{cosx}=2-\sqrt{1}=1\) khi \(cosx=1\Leftrightarrow x=k2\pi\).
\(1-cos^2x+1-cos^2y=\frac{1}{4}\Rightarrow cos^2x+cos^2y=\frac{7}{4}\)
\(\Rightarrow\frac{3}{4}\le cos^2x;cos^2y\le1\)
\(S=1+tan^2x+1+tan^2y-2=\frac{1}{cos^2x}+\frac{1}{cos^2y}-2\)
\(=\frac{7}{4cos^2x.cos^2y}-2=\frac{7}{4cos^2x\left(\frac{7}{4}-cos^2x\right)}-2=\frac{7}{-4cos^4x+7cos^2x}-2\)
Đặt \(cos^2x=t\) \(\Rightarrow\frac{3}{4}\le t\le1\)
Xét \(f\left(t\right)=-4t^2+7t\) trên \(\left[\frac{3}{4};1\right]\)
\(-\frac{b}{2a}=\frac{7}{8}\Rightarrow f\left(\frac{7}{8}\right)=\frac{49}{16}\) ; \(f\left(\frac{3}{4}\right)=3\); \(f\left(1\right)=3\)
\(\Rightarrow3\le f\left(t\right)\le\frac{49}{16}\)
\(\Rightarrow\frac{7}{\frac{49}{16}}-2\le S\le\frac{7}{3}-2\Leftrightarrow\frac{2}{7}\le S\le\frac{1}{3}\)
Không có trong đáp án?
Chọn D
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có
Do đó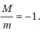
. Vì vậy, mệnh đề D sai.