Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
mk làm trên facebook, đo khó vẽ hình trên đây lại ko paste được hình lên nữa. Nick face là Cung Lâm Thiên Quốc. Mong bạn thông cảm cho.!!!!!!!!
Dưới đây là lời giải siêu gọn, đúng trọng tâm cho từng ý:
Cho: Hình bình hành \(A B C D\),
\(K , I\) là trung điểm của \(A B , C D\);
\(M , N\) là giao điểm của \(A I , C K\) với đường chéo \(B D\).
a) \(A K C I\) là hình bình hành
Vì \(K , I\) là trung điểm \(A B , C D\) ⇒ \(K I \parallel A C\), \(K I = \frac{1}{2} A C\)
Tương tự \(A C \parallel K I\), hai cặp cạnh đối song song ⇒
✅ \(A K C I\) là hình bình hành.
b) \(\angle M A C = \angle N C A\) và \(I M \parallel C N\)
- \(A K C I\) là hình bình hành ⇒ \(A I \parallel C K\)
⇒ \(I M \parallel C N\) (do cùng cắt \(B D\)) - Tam giác \(M A C\) và \(N C A\) có chung \(A C\), hai góc bằng nhau ⇒
✅ \(\angle M A C = \angle N C A\)
c) \(D M = M N = N B\)
- Do \(A I , C K\) cắt nhau tại trung điểm đường chéo trong hình bình hành, chia \(B D\) thành 3 đoạn bằng nhau
⇒ ✅ \(D M = M N = N B\)
d) \(A C , B D , I K\) đồng quy
- \(I K\) nối trung điểm \(A B , C D\) ⇒ là đường trung bình
- Đường chéo \(A C\) cắt \(I K\) tại 1 điểm
- \(B D\) cũng cắt tại điểm đó (do đối xứng trung điểm)
⇒ ✅ \(A C , B D , I K\) đồng quy
Xong! Gọn – đủ – đúng 😎
Cần vẽ hình không?
a: Ta có: \(AK=KB=\frac{AB}{2}\)
\(DI=IC=\frac{DC}{2}\)
mà AB=DC
nên AK=KB=DI=IC
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
b: Ta có: AKCI là hình bình hành
=>AI//CK
=>\(\hat{IAC}=\hat{KCA}\)
=>\(\hat{MAC}=\hat{NCA}\)
AI//CK
=>IM//CN
c: Xét ΔDNC có
I là trung điểm của DC
IM//NC
Do đó: M là trung điểm của DN
=>DM=MN
Xét ΔABM có
K là trung điểm của BA
KN//AM
Do đó: N là trung điểm của BM
=>BN=NM
=>BN=NM=DM
d: Ta có: AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(1)
ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,KI,BD đồng quy
A B C D M N o G G'
Gọi O là giao điểm của AC và BD => O là trung điểm AC (1), O là trung điểm BD(2)
Gọi G là giao điểm của AN và BD
N là trung điểm DC (3)
Từ (1), (3) => G là trọng tâm tam giác ADC => DG=2/3DO=\(\frac{2}{3}.\frac{1}{2}\)BC=1/3 BC
Tương tự gọi G' là giao điểm của AM và BD ta có G' là trọng tâm tam giác ABC=>BG"=2/3 BO=1/3BD
=>GG'=1/3 DB
=> DG=GG'=G'B
Xét tam giác ABC có :
AM và BO là 2 đường trung tuyến .
Áp dụng tính chất trọng tâm của 1 tam giác và tính chất 2 đường chéo trong hình bình hành ta có :
\(BF=\frac{2}{3}BO=\frac{2}{3}\times\frac{1}{2}BD=\frac{1}{3}BD\)
Xét tam giác ADC có :
\(DE=\frac{1}{3}BD\)
\(\Rightarrow EF=\frac{1}{3}BD\)
Và \(BF=FE=ED\)( đpcm)
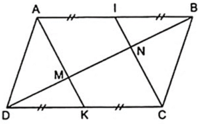
Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
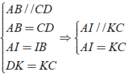
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.