Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó 
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà 
nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
| 9999973 |
9999983 |
9999993 |
| Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi A là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra 
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó 
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà 90000 = 70x128571 + 30, nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
| 9999973 |
9999983 |
9999993 |
| Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra 
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó 
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà 
nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
| 9999973 |
9999983 |
9999993 |
| Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi A là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra 
Đáp án D
Số phần tử của E là 
Trong E có 6 số chia hết cho 10 là 10, 20, 30, 40, 50, 60.
Số cách lấy ngẫu nhiên đồng thời hai phần tử trong E là 
cặp.
Biến cố M “lấy được ít nhất một số chia hết cho 10” gồm 
cách lấy được 2 số chia hết cho 10 và 
cách lấy được 1 số chia hết cho 10 và 1 số không chia hết cho 10.
Vậy số phần tử của biến cố M là
Đáp án A.
Gọi số cần tìm có dạng a b c d vì chia hết cho 6
⇒ d = { 2 , 4 , 6 , 8 } a + b + c + d : 3
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1 → 9).
+) Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .
Chọn A
+ Ta có 
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà 
nên c có 3 cách chọn.
Ta có: 
Xác suất cần tìm là: 
Chọn A
Số phần tử không gian mẫu: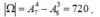
TH1: Nếu a = 2
b = 0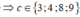
có 4 cách;d có 4 cách.
Vậy có 16 số.
có 5 cách;c có 5 cách; d có 4 cách.
Vậy có 100 số.
TH2: Nếu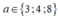
có 3 cách; b có 6 cách; c có 5 cách; d có 4 cách.
Vậy có 360 số.
TH3: Nếu a = 9
b = 0;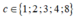
có 5 cách; d có 4 cách.
Vậy có 20 số.
Kết luận: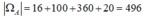
số