Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
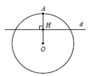
Khi quay hình tròn C quay trục OA ta được khối cầu có thể tích V = 4 3 π R 3 = 36 π
Khối tròn xoay H 1 chưa điểm A chính là chỏm cầu có chiều cao x 2 + 4
Suy ra thể tích khối H 1 là V 1 = π h 2 R − h 3 = π . A H 2 . 3 − A H 3
Mà V = V 1 + V 2 và
V 2 = 2 V 1 ⇒ V 1 V = 1 3 = A H 2 . 3 − A H 3 36 = 1 3 ⇔ A H 3 − 9 A H 2 + 36 = 0 *
Vì 0 < A H < O A = 3 nên giải * → c a s i o A H ≈ 2 , 32

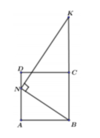
a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

Phương pháp:
Công thức tính thể tích của khối trụ có bán kính đáy R và chiều cao h: V = π R 2 h
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
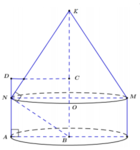
Khi quay tứ giác ANKB quanh trục BK ta được hình trụ có bán kính đáy AB, chiều cao AN và hình nón có bán kính đáy AB, chiều cao K O = B K − A N
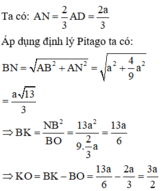
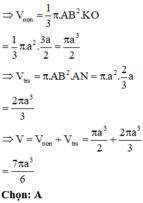

Đáp án B.
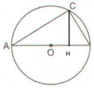
Quay tam giác AHC quanh trục AB thu được hình nón có h = AH; r = CH.



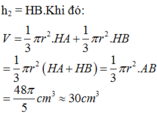


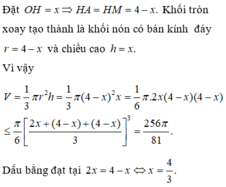
Đáp án B
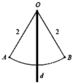
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24
Đáp án B
Giari thích các bước :
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24