Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: 
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: 
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: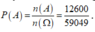 
Chọn A
+ Số các chỉnh hợp chập của tập hợp các chữ số 
Số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} mà chữ số 0 đứng vị trí đầu tiên ( 0 b c ¯ ) bằng số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} và bằng A 9 2 .
Suy ra số các số tự nhiên có chữ số đôi một khác nhau bằng 
+ Lấy ngẫu nhiên ra từ hai số có 
cách.
+ Gọi là biến cố “lấy được từ hai số mà các chữ số có mặt ở hai số đó giống nhau”
Trường hợp 1: Ba chữ số có mặt trong hai số được lấy không có chữ số 0
Chọn ba chữ số trong tập {0;1;2;3;4;5;6;7;8;9} có C 9 3 cách.
Ba chữ số này tạo thành 3! = 6 số trong A.
Lấy hai số trong 6 số này có C 6 2 cách (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 3 . C 6 2 cách lấy hai số thỏa trường hợp 1.
Trường hợp 2: Ba chữ số có mặt trong hai số được lấy có chữ số .
Chọn thêm hai chữ số trong tập {0;1;2;3;4;5;6;7;8;9}có C 9 2 cách.
Ba chữ số này (hai chữ số vừa chọn và chữ số 0) tạo thành 2.2! = 4 số trong A.
Lấy hai số trong 4 số này có C 4 2 (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 2 . C 4 2 cách lấy hai số thỏa trường hợp 2.
Suy ra 
+ Do đó, xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau là:
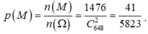
"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?
Chọn C
Gọi x là số bi của hộp thứ nhất nên số bi ở hộp thứ hai là 20 - x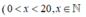
)
Gọi a,b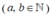
lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
Suy ra: 0 < a < x, 0 < b < 20 - x
Số cách lấy bi ở mỗi hộp là độc lập với nhau nên ta đặt:
+) Xác suất lấy một bi xanh ở hộp thứ nhất là a x và ở hộp thứ hai là b 20 - x
Với a, b, x là các số tự nhiên thỏa mãn
+) Xác suất lấy được hai bi xanh
Ta có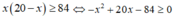
Lập bảng thử từng giá trị
Khi đó, các giá trị của x là 6 hoặc 84
Ta lại có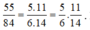
Do đó,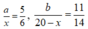
hoặc ngược lại
Vậy xác suất để lấy được hai viên bi đỏ là