Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Số các chỉnh hợp chập của tập hợp các chữ số ![]()
Số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} mà chữ số 0 đứng vị trí đầu tiên ( 0 b c ¯ ) bằng số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} và bằng A 9 2 .
Suy ra số các số tự nhiên có chữ số đôi một khác nhau bằng ![]()
+ Lấy ngẫu nhiên ra từ hai số có ![]() cách.
cách.
+ Gọi là biến cố “lấy được từ hai số mà các chữ số có mặt ở hai số đó giống nhau”
Trường hợp 1: Ba chữ số có mặt trong hai số được lấy không có chữ số 0
Chọn ba chữ số trong tập {0;1;2;3;4;5;6;7;8;9} có C 9 3 cách.
Ba chữ số này tạo thành 3! = 6 số trong A.
Lấy hai số trong 6 số này có C 6 2 cách (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 3 . C 6 2 cách lấy hai số thỏa trường hợp 1.
Trường hợp 2: Ba chữ số có mặt trong hai số được lấy có chữ số .
Chọn thêm hai chữ số trong tập {0;1;2;3;4;5;6;7;8;9}có C 9 2 cách.
Ba chữ số này (hai chữ số vừa chọn và chữ số 0) tạo thành 2.2! = 4 số trong A.
Lấy hai số trong 4 số này có C 4 2 (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có C 9 2 . C 4 2 cách lấy hai số thỏa trường hợp 2.
Suy ra ![]()
+ Do đó, xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau là:
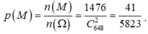

- Có 5 cách chọn chữ số hàng trăm.
- Có 5 cách chọn chữ số hàng chục.
- Có 4 cách chọn chữ số hàng đơn vị.
Số số được tạo thành là:
\(5.5.4=100\) (số)
Tuy nhiên trong 100 số này đã bị mất đi 1 số số chẵn:
| 012 | 013 | 014 | 015 |
| 021 | 023 | 024 | 025 |
| 031 | 032 | 034 | 035 |
| 041 | 042 | 043 | 045 |
| 051 | 052 | 053 | 054 |
Vậy số số lẻ hơn số số chẵn là 8 số.
Có số số chẵn là:
\(\left(100-8\right):2=46\) (số)
Có số số lẻ là :
\(100-46=54\) (số)
Nếu coi 100 số là 100 %.
Xác xuất chọn được số chẵn ở lần chọn đầu là:
\(46:100.100=46\%\)
Xác xuất chọn được số chẵn ở lần chọn thứ 2 (nếu lần ko trúng) là:
\(46:99.100\approx46,5\)

GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG

Chọn C
Gọi x là số bi của hộp thứ nhất nên số bi ở hộp thứ hai là 20 - x ![]() )
)
Gọi a,b ![]() lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
Suy ra: 0 < a < x, 0 < b < 20 - x
Số cách lấy bi ở mỗi hộp là độc lập với nhau nên ta đặt:
+) Xác suất lấy một bi xanh ở hộp thứ nhất là a x và ở hộp thứ hai là b 20 - x
Với a, b, x là các số tự nhiên thỏa mãn ![]()
+) Xác suất lấy được hai bi xanh 
Ta có ![]()
![]()
Lập bảng thử từng giá trị


Khi đó, các giá trị của x là 6 hoặc 84
Ta lại có 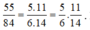
Do đó, ![]() hoặc ngược lại
hoặc ngược lại
Vậy xác suất để lấy được hai viên bi đỏ là
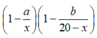
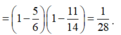

Chọn D
*) Ta có: ![]()
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có ![]() (cách).
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có ![]() cách.
cách.
Xếp hai chữ số 2 đứng liền nhau: Có ![]() cách.
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: ![]() (cách)
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: ![]() (cách)
(cách)
Vậy ![]()
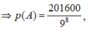


Đáp án A.