K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
V
2
13 tháng 8 2016
PT <=> 2016x(x-√(4x-3)) + (x-√(4x-3))(x+√(4x-3))=0
<=> (x-√(4x-3))(2016+x+√(4x-3))=0
Còn lại bạn tự giải
T
4 tháng 12 2016
112345678996578452062752965856*75461852145363625432863963978=112345678996578452062752965856*75461852145363625432863963978=
15 tháng 7 2020
x2 + 2y2 + 2xy + 3y - 4 = 0
<=> 4x2 + 8y2 + 8xy + 12y - 16 = 0
<=> (4x2 + 8xy + 4y2) + (4y2 + 12y + 9) = 25
<=> (2x+ 2y)2 + (2y + 3)2 = 25 = 0 + 52 = 32 + 42
Do x;y là số nguyên và 2y + 3 là số lẻ => (2y + 3)2 thuộc {52; 32}
Xét các TH xảy ra:
+)\(\hept{\begin{cases}2x+2y=0\\2y+3=5\end{cases}}\) <=> \(\hept{\begin{cases}x+y=0\\y=1\end{cases}}\) <=> \(\hept{\begin{cases}x=-1\\y=0\end{cases}}\)
+) \(\hept{\begin{cases}2x+2y=0\\2y+3=-5\end{cases}}\)
+) \(\hept{\begin{cases}2x+2y=4\\2y+3=3\end{cases}}\)
+) \(\hept{\begin{cases}2x+2y=-4\\2y+3=-3\end{cases}}\)
+) \(\hept{\begin{cases}2x+2y=4\\2y+3=-3\end{cases}}\)
+) \(\hept{\begin{cases}2x+2y=-4\\2y+3=3\end{cases}}\)
(Tự tính x;y)
29 tháng 6 2020
Ta có:
\(P=\frac{x+12}{\sqrt{x}+2}=\sqrt{x}-2+\frac{16}{\sqrt{x}+2}\)
\(=\left(\sqrt{x}+2\right)+\frac{16}{\sqrt{x}+2}-4\ge2\sqrt{\left(\sqrt{x}+2\right).\frac{16}{\sqrt{x}+2}}-4=4\)
Dấu "=" xảy ra <=> \(\sqrt{x}+2=\frac{16}{\sqrt{x}+2}\Leftrightarrow\sqrt{x}+2=4\Leftrightarrow x=4\) thỏa mãn
=> min P = 4 tại x = 4.
TA
9 tháng 5 2018
Tìm số nghiệm của PT thì mình biết chứ mấy cái tìm Min hay Max thì bạn xem đây nhé: https://cunghoctot.vn/Lesson/Detail/ki-nang-tim-gtnn-va-gtln-bang-3095
Tìm số nghiệm có 2 dạng:
1 là tìm nghiệm của PT bậc nhất
2 là tìm nghiệm của PT bậc 2 hoặc cao hơn
Đối với PT bậc nhất: VD: \(2x+5=6\)
Bạn bấm vào máy \(2x+5=6\) (đừng nói là bạn cũng không biết ghi nhé ^-^ )
Sau đó bấm các phím: SHIFT + CALC (tức là giải PT : SOLVE)
Màn hình sẽ hiện ra dòng chữ: Solve for X
Bạn ấn dấu "=" máy sẽ giải PT đó và cho ra kết quả
\(X=0.5\) (bạn không cần quan tâm đến dòng \(L-R=0\) đâu nhé, vì đó là phần lên cấp 3 mới học)
Giờ đến PT bậc 2
Bạn cũng có thể làm các bước như vừa rồi nếu PT có nghiệm kép
Còn muốn chắc chắn thì làm như sau:
Bạn bấm các phím: MODE + 5:EQN
Đến đây có 4 số 1 2 3 4:
Số 1 dùng cho giải hệ phương trình
Số 2 dùng để giải PT có 3 ẩn
Số 3 dùng để giải PT bậc 2
Số 4 dùng để giải PT bậc 3
Đối với số 1, bạn chỉ cần bấm các số vào và dùng dấu "=" để máy ghi nhớ
VD: \(\begin{cases}3x+y=3\\2x-y=7\end{cases}\)
Bạn bấm như sau (Từ trái sang phải nhé): \(1a=3\) ; \(1b=1\) ; \(1c=3\) ; \(2a=2\) ; \(2b=-1\) ; \(2c=7\)
Rồi bấm dấu "=", sẽ ra được: \(x=2\) và \(y=-3\)
Đó là đối với hệ phương trình có nghiệm, còn với vô số nghiệm thì nó sẽ ra dòng chữ: Infinite Sol và với vô nghiệm là: No-Solution
Đối với số 2, thì bạn cũng làm tương tự như với số 1
Đối với số 3, bạn cũng làm như bình thường
Nhập số vào, bấm dấu"="
Đến đây màn hình sẽ ra kết quả:
Nếu có \(x_1,x_2\) (tức là bấm dấu "=" rồi bấm thêm 1 lần nữa) thì PT có 2 nghiệm
Nếu chỉ ghi \(x\) thì PT có nghiệm kép
Nếu ra \(x_1,x_2\) nhưng lại ra số có chữ "i" trong đó tức là PT vô nghiệm (VD: \(x_1=-\dfrac{1}{3}+\dfrac{\sqrt{2}}{3}i\) ; \(x_2=-\dfrac{1}{3}-\dfrac{\sqrt{2}}{3}i\) )
Đối với số 4 thì cũng tương tự như các số trên
15 tháng 3 2022
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{4}{\sqrt{x}\left(\sqrt{x}-3\right)}\right).\left(\dfrac{\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right)\)
\(=\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}+3\right)}.\left(\dfrac{2\sqrt{x}}{x-4}\right)=\dfrac{2}{\sqrt{x}+3}\)
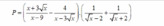
1.46 \(a,P=\frac{\sqrt{x}+1}{\sqrt{x}-2}+\frac{2\sqrt{x}}{\sqrt{x}+2}+\frac{2+5\sqrt{x}}{4-x}\)
\(P=\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\frac{2+5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(P=\frac{x+3\sqrt{x}+2+2x-2\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(P=\frac{3x-4\sqrt{x}}{x-4}\)
gọn quá