
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



c: Xét ΔBKC có
BH,CA là đường cao
BH cắt CA tại I
=>I là trực tâm
=>KI vuông góc BC tại D
góc DAC=góc DAI=góc HBC
góc HAC=góc DKC
mà góc HBC=góc DKC
nên góc DAC=góc HAC
=>AC là phân giác của góc DAH

a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
BA=BM
Do đó: ΔBAD=ΔBMD
Suy ra: DA=DM
Xét ΔADE vuông tại A và ΔMDC vuông tại M có
DA=DM
\(\widehat{ADE}=\widehat{MDC}\)
Do đó: ΔADE=ΔMDC
Suy ra: AE=MC
Ta có: BA+AE=BE
BM+MC=BC
mà BA=BM
và AE=MC
nên BE=BC

đầu tiên là gọi ẩn
xong rồi lập phương trình theo những dữ kiện đề bài cho
và cuối cùng là giải phương trình và lấy nghiệm thỏa mãn điều kiện ban đầu của ẩn
1. Gọi ẩn và đặt điều kiện cho ẩn
2. Lập phương trình theo dữ liệu trong đề bài
3. Giải phương trình và trả lời bài toán


a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE

b: AF*AB=AE*AC
=>AF/AC=AE/AB
mà góc A chung
nên ΔAFE đồng dạng với ΔACB
=>góc AFE=góc ACB

\(\dfrac{a}{bc}+\dfrac{b}{ac}>=2\cdot\sqrt{\dfrac{a}{bc}\cdot\dfrac{b}{ac}}=\dfrac{2}{cc}\)
\(\dfrac{b}{ca}+\dfrac{c}{ab}>=2\cdot\sqrt{\dfrac{bc}{ca\cdot ab}}=\dfrac{2}{a}\)
\(\dfrac{c}{ab}+\dfrac{a}{bc}>=2\cdot\sqrt{\dfrac{a\cdot c}{a\cdot b\cdot c\cdot b}}=\dfrac{2}{b}\)
=>a/bc+b/ac+c/ab>=2(1/a+1/b+1/c)

Tổng thời gian đi và về là: 9h30'-7h-15 phút = 2h15' = 9/4h
Gọi quãng đường AB là x(x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{50}\left(h\right)\)
Thời gian đi từ A đến B là \(\dfrac{x}{40}\left(h\right)\)
Theo bài ra ta có pt:
\(\dfrac{x}{50}+\dfrac{x}{40}=\dfrac{9}{4}\\ \Leftrightarrow\dfrac{4x}{200}+\dfrac{5x}{200}=\dfrac{450}{200}\\ \Leftrightarrow9x=450\\ \Leftrightarrow x=50\left(tm\right)\)
Vậy quãng đường AB là 50 km


 giups mình với các bạn mình đang cần gấp để nộp bài
giups mình với các bạn mình đang cần gấp để nộp bài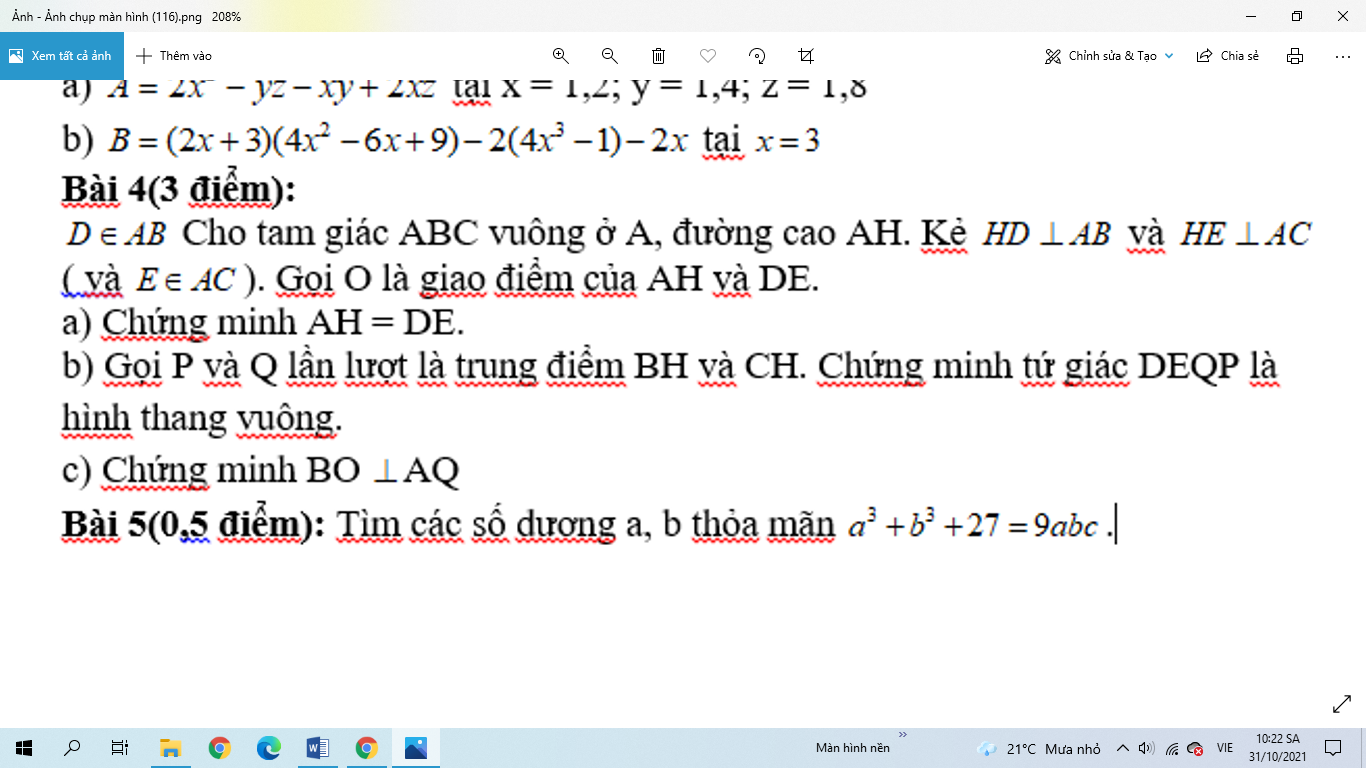
 Giups mình câu b ạ
Giups mình câu b ạ