Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đoạn thẳng f: Đoạn thẳng [A, C] Đoạn thẳng h: Đoạn thẳng [A, B] Đoạn thẳng i: Đoạn thẳng [C, B] Đoạn thẳng m: Đoạn thẳng [E, H] Đoạn thẳng n: Đoạn thẳng [F, H] Đoạn thẳng p: Đoạn thẳng [A, H] Đoạn thẳng q: Đoạn thẳng [A, M] A = (-1.98, 1.26) A = (-1.98, 1.26) A = (-1.98, 1.26) C = (7.12, 1.2) C = (7.12, 1.2) C = (7.12, 1.2) Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm H: Giao điểm đường của j, i Điểm H: Giao điểm đường của j, i Điểm H: Giao điểm đường của j, i Điểm E: Giao điểm đường của k, h Điểm E: Giao điểm đường của k, h Điểm E: Giao điểm đường của k, h Điểm F: Giao điểm đường của l, f Điểm F: Giao điểm đường của l, f Điểm F: Giao điểm đường của l, f Điểm M: Trung điểm của B, C Điểm M: Trung điểm của B, C Điểm M: Trung điểm của B, C
a) Xét tam giác AEH và tam giác AHB có:
\(\widehat{AEH}=\widehat{AHB}=90^o\)
Góc A chung
\(\Rightarrow\Delta AEH\sim\Delta AHB\left(g-g\right)\Rightarrow\frac{AH}{AB}=\frac{AE}{AH}\Rightarrow AE.AB=AH^2\)
Tương tự \(\Delta AHF\sim\Delta ACH\left(g-g\right)\Rightarrow\frac{AH}{AC}=\frac{AF}{AH}\Rightarrow AF.AC=AH^2\)
Xét tam giác vuông ABC có AH là đường cao nên áp dụng hệ thức lượng trong tam giác ta có:
\(HB.HC=AH^2\)
Vậy nên ta có AE.AB = AF.AC = HB.HC
b) Ta có \(\Delta AHC\sim\Delta BAC\left(g-g\right)\Rightarrow\frac{AH}{AB}=\frac{HC}{AC}\Rightarrow AH.AC=AB.HC\)
\(\Rightarrow AB.AH.AC=AB.AB.HC\Rightarrow\left(AB.AC\right).AH=AB^2.HC\)
\(\Rightarrow BC.AH.AH=AB^2.HC\Rightarrow AH^2.BC=AB^2.HC\)
\(\Rightarrow\frac{AH^2}{AB^2}=\frac{CH}{BC}\Rightarrow\left(\frac{AH}{AB}\right)^2=\frac{CH}{BC}\Rightarrow sin^2B=\frac{CH}{BC}\)
c) Xét tam giác vuông ABC có AH là đường cao, áp dụng hệ thức lượng trong tam giác ta có :
\(AC^2=HC.BC\)
Lại có AM là đường trung tuyến ứng với cạnh huyền nên BC = 2AM.
Suy ra \(AC^2=HC.2.AM\Rightarrow\frac{1}{AM}=\frac{2HC}{AC^2}\Rightarrow\frac{AH}{AM}=2.\frac{AH}{AC}.\frac{HC}{AC}\)
\(\Rightarrow sin\widehat{AMB}=2.sin\widehat{ACB}.cos\widehat{ACB}\)

\(cosB=\frac{AB}{BC}=\frac{AB}{12}=\frac{3}{5}\Rightarrow AB=\frac{36}{5}\)
Tam giác ABC vuông tại A nên theo định lý Py-ta-go, ta có: \(AC=\sqrt{BC^2-AB^2}=\sqrt{12^2-\left(\frac{36}{5}\right)^2}=\frac{48}{5}\)
Ta có: \(cosB=\frac{3}{5}\)ta dùng máy tính bỏ túi tìm được \(\widehat{B}\approx53^0\), do đó \(\widehat{C}\approx90^0-53^0=37^0\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)

a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
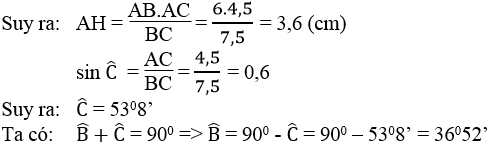 b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
