K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
2
Giups mik chỗ này nó lỗi ko đánh đc11 tháng 12 2021
\( (-11).77 - 23.11 + (-29) \)
\(=11.(-77)-23.11+(-29)\)
\(=11.[(-77)-23]+(-29)\)
\(=11.(-100)+(-29)\)
= -1100 + (-29)
= -(1100+29)=-1071
Mik đang cần gấp tr 4h30 chiều nay!! Giups mik vs ạ
6 tháng 1 2022
Câu 2:
1: \(\Leftrightarrow x\cdot\dfrac{7}{2}=\dfrac{9}{2}+3=\dfrac{15}{2}\)
hay x=15/7
2: \(\Leftrightarrow x=\dfrac{5}{2}\cdot\dfrac{8}{5}=4\)
3: \(\Leftrightarrow x=\dfrac{-11\cdot10}{5}=-11\cdot2=-22\)
4: =>2x=90
hay x=45
NN
Giups mik tr 3h đc ko ạ? Mik cần gấp......
2
TD
1 tháng 4 2023
a,Trên tia Ox vì OA<OB nên trong 3 điểm O,A,B là điểm A nằm giữa 2 điểm còn lại.Hai điểm A và O nằm cùng phía với điểm B
b, Vì A nằm giữa đoạn thẳng OB
Nên Độ dài AB=OB-OA
=7-3,5
= 3,5 cm
c,Vì điểm A nằm giữa đoạn thẳng OB
Mà OA=AB=\(\dfrac{OB}{2}\)
Nên A là trung điểm đoạn thẳng OB
d,Vì M là trung điểm đoạn thẳng
Nên OM=MC=\(\dfrac{OC}{2}\)
⇒OM=MC=8:2=4cm
Độ dài đoạn thẳng BM=OM+OB
=4+7
=11cm
e,Tên:IO,IM,IC,IA
f,Công thức tính đường thẳng =\(\dfrac{n.\left(n-1\right)}{2}\)
⇒\(\dfrac{n.\left(n-1\right)}{2}\)=131
n.(n-1)=262
n=16
Mình nghĩ vậy.chứ mình cảm giác đề bạn sai á!
LT
3
AO
19 tháng 2 2018
\(-52+\frac{2}{3}x=-46\)
\(\frac{2}{3}x=-46+52\)
\(\frac{2}{3}x=6\)
\(x=6:\frac{2}{3}\)
\(x=9\)
18 tháng 2 2022
Bài 8:
a: \(A=7\left(\dfrac{1}{10}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{12}+...+\dfrac{1}{69}-\dfrac{1}{70}\right)\)
\(=7\cdot\dfrac{6}{70}=\dfrac{6}{10}=\dfrac{3}{5}\)
b: \(B=2\left(\dfrac{1}{15}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{21}+...+\dfrac{1}{87}-\dfrac{1}{90}\right)\)
\(=2\left(\dfrac{1}{15}-\dfrac{1}{90}\right)\)
\(=2\cdot\dfrac{5}{90}=\dfrac{10}{90}=\dfrac{1}{9}\)
c: \(C=3\left(\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+\dfrac{1}{14}-...+\dfrac{1}{197}-\dfrac{1}{200}\right)\)
\(=3\cdot\dfrac{24}{200}=\dfrac{72}{200}=\dfrac{9}{25}\)
15 tháng 12 2023
k: \(\left(4x-16\right)\left(-72+9x\right)=0\)
=>\(4\cdot\left(x-4\right)\cdot9\left(x-8\right)=0\)
=>\(36\left(x-4\right)\left(x-8\right)=0\)
=>\(\left(x-4\right)\left(x-8\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=8\end{matrix}\right.\)
m: \(\left(20+5x\right)\left(4x-8\right)=0\)
=>\(5\cdot\left(x+4\right)\cdot4\left(x-2\right)=0\)
=>\(\left(x+4\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
n: \(\left(-4x+48\right)\left(2x-24\right)=0\)
=>\(-4\left(x-12\right)\cdot2\left(x-12\right)=0\)
=>\(\left(x-12\right)^2=0\)
=>x-12=0
=>x=12
o: \(\left(4x+16\right)\left(-2x+20\right)\left(-40+x\right)=0\)
=>\(4\cdot\left(x+4\right)\cdot\left(-2\right)\left(x-10\right)\left(x-40\right)=0\)
=>\(\left(x+4\right)\left(x-10\right)\left(x-40\right)=0\)
=>\(\left[{}\begin{matrix}x+4=0\\x-10=0\\x-40=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=10\\x=40\end{matrix}\right.\)
p: \(\left(-5x+40\right)\left(-x+2023\right)\left(2x-2\right)=0\)
=>\(-5\left(x-8\right)\cdot\left(-1\right)\cdot\left(x-2023\right)\cdot2\left(x-1\right)=0\)
=>\(\left(x-8\right)\left(x-2023\right)\left(x-1\right)=0\)
=>\(\left[{}\begin{matrix}x-8=0\\x-1=0\\x-2023=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=1\\x=2023\end{matrix}\right.\)
q: \(2024x\left(4x-8\right)\left(5+5x\right)=0\)
=>\(x\cdot4\left(x-2\right)\cdot5\left(x+1\right)=0\)
=>\(x\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-1\end{matrix}\right.\)
r: \(-4x\left(3x+9\right)\left(2x-16\right)=0\)
=>\(-4x\cdot3\left(x+3\right)\cdot2\left(x-8\right)=0\)
=>\(x\left(x+3\right)\left(x-8\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x+3=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=8\end{matrix}\right.\)
s: \(\left(-100+5x\right)\left(2x-10\right)\left(6x+6\right)=0\)
=>\(5\cdot\left(x-20\right)\cdot2\left(x-5\right)\cdot6\left(x+1\right)=0\)
=>\(\left(x-20\right)\left(x-5\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-20=0\\x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=5\\x=-1\end{matrix}\right.\)
t: \(\left(-2x+4\right)\left(2x+16\right)\cdot\left(7-x\right)=0\)
=>\(-2\left(x-2\right)\cdot2\left(x+8\right)\cdot\left(-1\right)\cdot\left(x-7\right)=0\)
=>\(\left(x-2\right)\left(x+8\right)\left(x-7\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x-7=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-8\\x=7\end{matrix}\right.\)
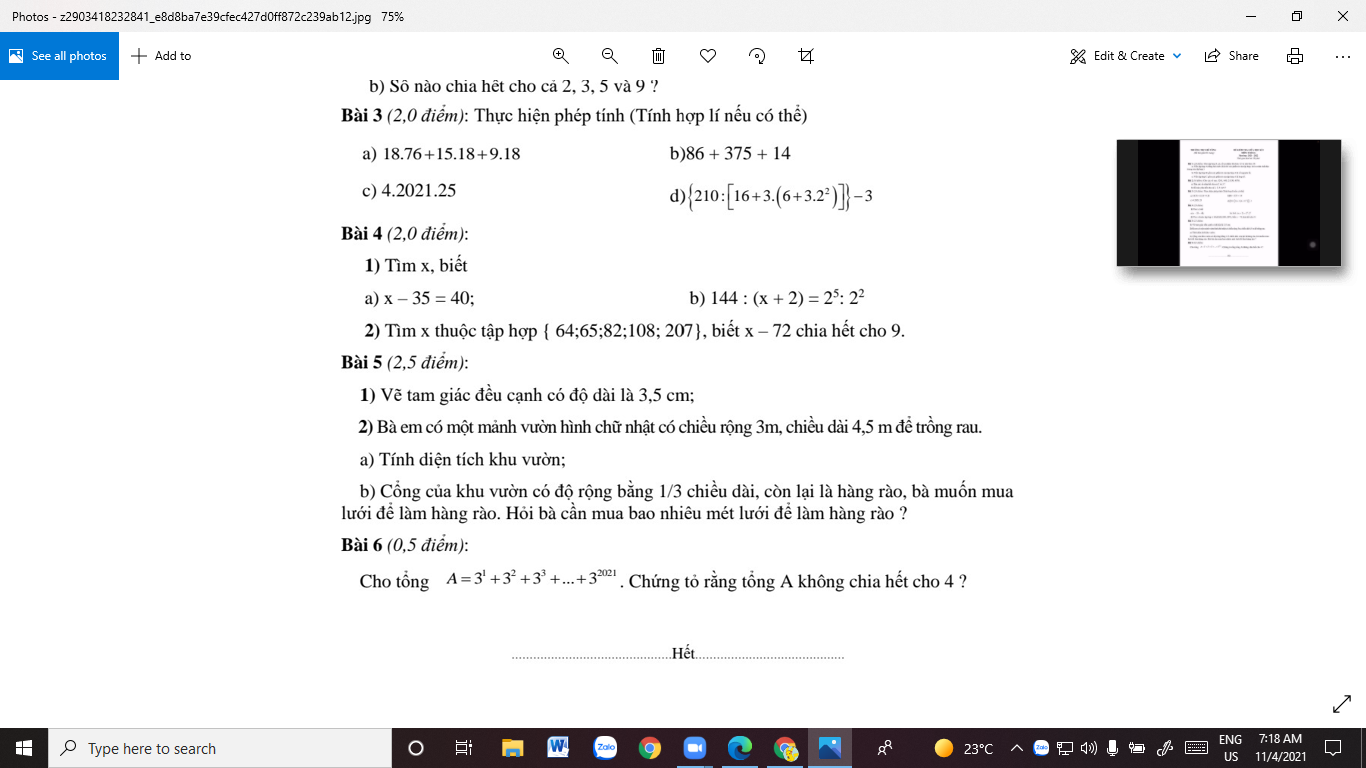
Bài 6:
\(A=3+\left(3^2+3^3\right)+\left(3^4+3^5\right)+...+\left(3^{2020}+3^{2021}\right)\\ A=3+3^2\left(1+3\right)+3^4\left(1+3\right)+...+3^{2021}\left(1+3\right)\\ A=3+4\left(3^2+3^4+...+3^{2021}\right)⋮̸4\left(3⋮̸4\right)\)
chacws chắn đúng chứ ạ ?