K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 2 2022
bạn đăng tách ra cho mn cùng giúp nhé
Bài 2 :
a, bạn tự vẽ
b, \(\left\{{}\begin{matrix}x^2-x-2=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1;x=2\\y=1;y=4\end{matrix}\right.\)
Vậy (d) cắt (P) tại A(-1;1) ; B(2;4)
2 tháng 9 2021
\(a) Đk:x<\dfrac{1}{2}\)
\(\sqrt{-2x+1}>7\)
\(\Leftrightarrow\)\(-2x+1>49\)
\(\Leftrightarrow\)\(x<-24\)
\(b)\)\(Đk:x>-9\)
\(\sqrt{x+9}\)\(\le\)\(31\)
\(\Leftrightarrow\)\(x+9\)\(\le\)\(961\)
\(\Leftrightarrow\)\(x\)\(\le\)\(952\)
\(c)\)Ta có:
\(-3\sqrt{3}=-\sqrt{27} \)
\(-2\sqrt{7}=-\sqrt{28}\)
\(-\sqrt{27}>-\sqrt{28}\)
\(\Rightarrow\)\(-3\sqrt{3}>-2\sqrt{7}\)
10 tháng 11 2021
\(9,\tan B=\dfrac{AC}{AB}=\dfrac{4}{3}\left(B\right)\\ 10,A=\dfrac{x-4\sqrt{x}+4\sqrt{x}+16}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\cdot\dfrac{\sqrt{x}+4}{x+16}\\ A=\dfrac{x+16}{\left(\sqrt{x}-4\right)\left(x+16\right)}=\dfrac{1}{\sqrt{x}-4}\left(A\right)\\ 11,B=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\left(x-1\right)^2}{2}\\ B=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)^2}{2}\\ B=\dfrac{-2\sqrt{x}\left(\sqrt{x}-1\right)}{2}=-\sqrt{x}\left(\sqrt{x}-1\right)\\ B>0\Leftrightarrow\sqrt{x}-1< 0\left(-\sqrt{x}< 0\right)\\ \Leftrightarrow0\le x< 1\left(D\right)\)
26 tháng 2 2022
\(a)\) Thay \(m=6\) vào phương trình (1), ta có:
\(x^2+x-6=0.\\ \Delta=1^2-4.1.\left(-6\right).\\ \Delta=25>0.\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt.
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-1+\sqrt{25}}{2.1}=\dfrac{-1+5}{2}=2.\\x_2=\dfrac{-1-\sqrt{25}}{2.1}=\dfrac{-1-5}{2}=-3.\end{matrix}\right.\)
\(b)\) Để phương trình (1) có 2 nghiệm phân biệt.
\(\Leftrightarrow\Delta>0\\ .\Leftrightarrow1^2-4.1.\left(-m\right)>0.\\ \Leftrightarrow1+4m>0.\\ \Leftrightarrow4m>-1.\\ \Leftrightarrow m>\dfrac{-1}{4}.\)
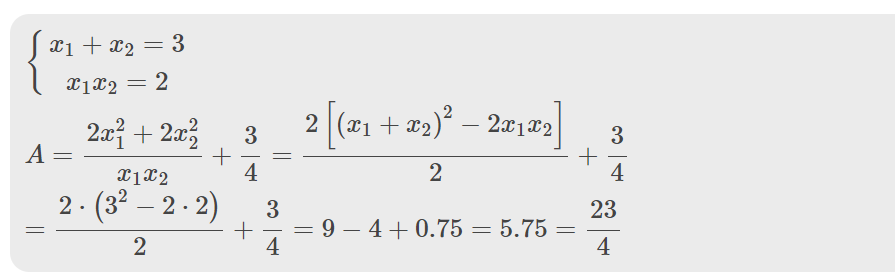
giúp mk cau b vs
TN
1
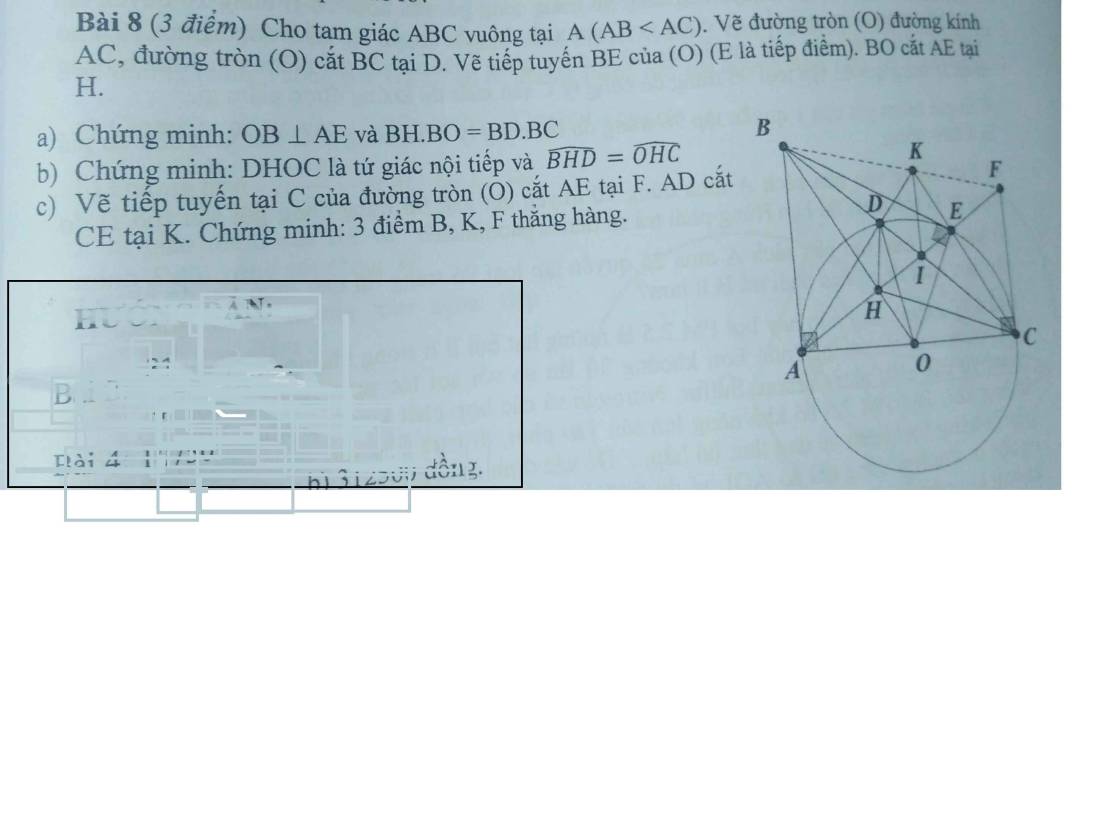
ồ cái này e chx học nhé chị