
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

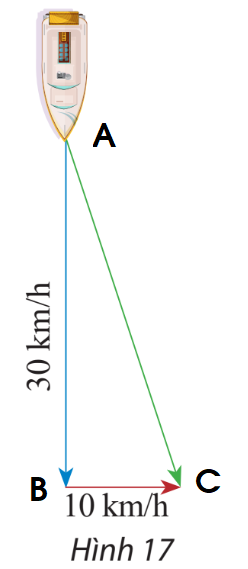
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

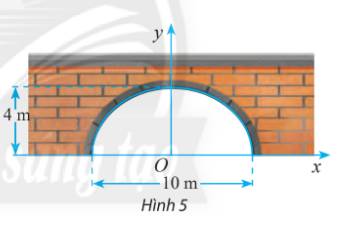
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là một tổ hợp chập 2 của 8.

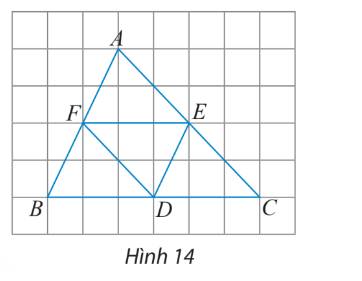
Từ giả thiết ta có:
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)
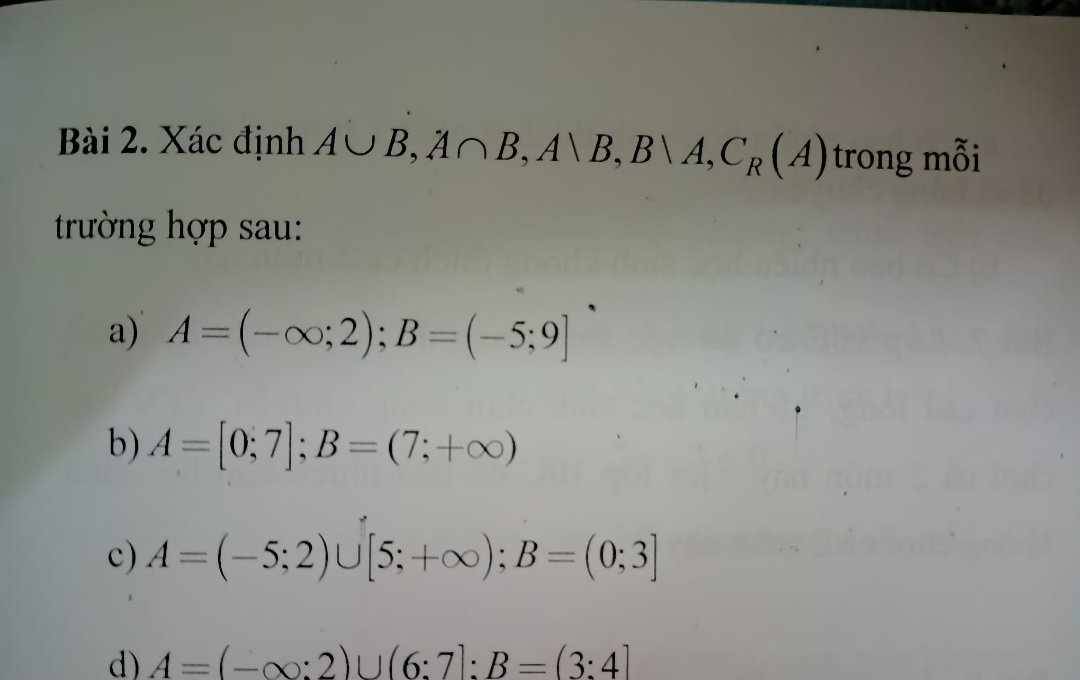 giup voiii
giup voiii



a: \(A=\left(-\infty;2\right);B=(-5;9]\)
A hợp B=(-vô cực;9]
A giao B=(-5;2)
A\B=(-vô cực;-5]
B\A=[2;9]
CRA=R\A=[2;+vô cực)
b: A=[0;7]; \(B=\left(7;+\infty\right)\)
A giao B=rỗng
A hợp B=[0;+vô cực)
A\B=[0;7]
B\A=(7;+vô cực)
CRA=R\A=(-vô cực;0) hợp (7;+vô cực)
c: \(A=\left(-5;2\right)\cup[5;+\infty);B=(0;3]\)
A giao B=(0;2)
A hợp B=(-5;2) hợp (0;3] hợp (5;+vô cực)
A\B=(-5;0] hợp [5;+vô cực]
B\A=[2;3]
CRA=R\A=(-vô cực;-5] hợp [2;5)
d: \(A=\left(-\infty;2\right)\cup(6;7];B=(3;4]\)
A hợp B=(-vô cực;2) hợp (3;4] hợp (6;7]
A giao B=rỗng
A\B=(-vô cực;2) hợp (6;7]
B\A=(3;4]
CRA=R\A=[2;6] hợp (7;+vô cực)