
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)



Xét (O) có
AB là tiếp tuyến có B là tiếp điểm
AC là tiếp tuyến có C là tiếp điểm
Do đó: AB=AC
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC

\(a,\sqrt{x^2+2x+1}-2x=1\\ \Leftrightarrow a,\left|x+1\right|=1+2x\left(x\ge-\dfrac{1}{2}\right)\\ \Leftrightarrow\left[{}\begin{matrix}x+1=1+2x\\x+1=-1-2x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-\dfrac{2}{3}\left(ktm\right)\end{matrix}\right.\)
b,ĐKXĐ:\(x\ge-2\)
\(\sqrt{x^2-8x+16}=x+2\\ \Leftrightarrow\left|x-4\right|=x+2\\ \Leftrightarrow\left[{}\begin{matrix}x-4=x+2\\x-4=-x-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}6=0\left(vô.lí\right)\\x=1\left(tm\right)\end{matrix}\right.\)
\(a,PT\Leftrightarrow\left|x+1\right|=2x+1\\ \Leftrightarrow\left[{}\begin{matrix}x+1=2x+1\left(x\ge-1\right)\\-x-1=2x+1\left(x< -1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-\dfrac{2}{3}\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=0\\ b,PT\Leftrightarrow\left|x-4\right|=x+2\\ \Leftrightarrow\left[{}\begin{matrix}x-4=x+2\left(x\ge4\right)\\4-x=x+2\left(x< 4\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\\x=1\left(tm\right)\end{matrix}\right.\Leftrightarrow x=1\)


Bài 5:
\(P=\left(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\dfrac{a+2}{a-2}\) (đk:\(a>0;a\ne2;a\ne1\))
\(=\left(\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\right).\dfrac{a-2}{a+2}\)
\(=\left(\dfrac{a+\sqrt{a}+1}{\sqrt{a}}-\dfrac{a-\sqrt{a}+1}{\sqrt{a}}\right).\dfrac{a-2}{a+2}\)
\(=\left(\sqrt{a}+1+\dfrac{1}{\sqrt{a}}-\sqrt{a}+1-\dfrac{1}{\sqrt{a}}\right).\dfrac{a-2}{a+2}\)
\(=\dfrac{2\left(a-2\right)}{a+2}\)
b) \(P=\dfrac{2\left(a-2\right)}{a+2}=\dfrac{2\left(a+2\right)-8}{a+2}=2-\dfrac{8}{a+2}\)
Để \(P\in Z\) \(\Leftrightarrow\dfrac{8}{a+2}\in Z\)
Có \(a\in Z,a>0\) \(\Rightarrow a+2\in Z\) và \(a+2>2\)
=> \(a+2\inƯ\left(8\right)=\left\{4;8\right\}\) \(\Leftrightarrow a\in\left\{2;6\right\}\) mà a\(\ne2\) =>a=6
Vậy a=6


a: \(\sqrt{3}-2=\sqrt{3}-\sqrt{4}< 0\)
=>Hàm số \(y=\left(\sqrt{3}-2\right)x+3\) nghịch biến trên R
a: Khi \(x=2+\sqrt{3}\) thì
\(y=\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)+3\)
=3-4+3
=6-4
=2
b: Thay \(y=\sqrt{3}+1\) vào \(y=\left(\sqrt{3}-2\right)x+3\), ta được:
\(x\left(\sqrt{3}-2\right)+3=\sqrt{3}+1\)
=>\(x\left(\sqrt{3}-2\right)=\sqrt{3}-2\)
=>x=1

a: Vì (d)//y=3x nên m-1=3
hay m=2
Vậy: (d): y=3x+2n-5
Thay x=1 và y=4 vào (d), ta được:
2n-5+3=4
\(\Leftrightarrow2n=6\)
hay n=3






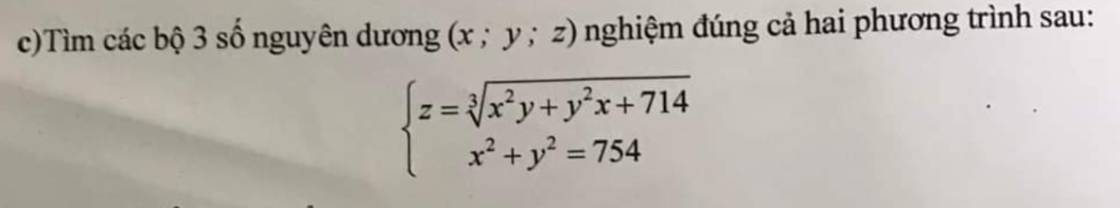
 giúp mik với mn ơi
giúp mik với mn ơi 
lỗi hả