
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBAC có
D là trung điểm của AB
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//BC và \(DM=\dfrac{BC}{2}=3.5\left(cm\right)\)

Bài 4:
a: \(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
=-8

11) 3x(x-5)2-(x+2)3+2(x-1)3-(2x+1)(4x2-2x+1)=3x(x2-10x+25)-(x3+6x2+12x+8)+2(x3-3x2+3x-1)-(8x3+1)=3x3-30x2+75x-x3-6x2-12x-8+2x3-6x2+6x-2-8x3-1=-4x3-42x2+63x-11

\(M=35\left(6^2+1\right)\left(6^4+1\right)\left(6^8+1\right)\left(6^{12}+1\right)-6^{24}\)
\(=\left(6^2-1\right)\left(6^2+1\right)\left(6^4+1\right)\left(6^8+1\right)\left(6^{12}+1\right)-6^{24}\)
\(=\left(6^4-1\right)\left(6^4+1\right)\left(6^8+1\right)\left(6^{12}+1\right)-6^{24}\)
\(=6^{24}-1-6^{24}=-1\)
\(M=\left(6^2-1\right)\left(6^2+1\right)\left(6^4+1\right)\left(6^8+1\right)\left(6^{12}+1\right)-6^{24}\)
\(=\left(6^4-1\right)\left(6^4+1\right)\left(6^8+1\right)\left(6^{12}+1\right)-6^{24}\)
\(=\left(6^8-1\right)\left(6^8+1\right)\left(6^{12}+1\right)-6^{24}\)
\(=\left(6^{16}-1\right)\left(6^{12}+1\right)-6^{24}\)
\(=6^{28}+6^{16}-6^{12}-1-6^{24}\)


c: \(\dfrac{2}{x-1}=\dfrac{2x+2}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{2}{x+1}=\dfrac{2x-2}{\left(x+1\right)\left(x-1\right)}\)
\(\dfrac{1}{x^2-1}=\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)


a. Áp dụng BĐT Bunhiacopxky:
$\text{VT}^2\leq [(a+2)+(b+2)+(c+2)](1+1+1)=3(a+b+c+6)=3.12=36$
$\Rightarrow \text{VT}\leq 6$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=2$
b.
Áp dụng BĐT Cô-si:
$\text{VT}\leq \frac{a+3b+8+8}{12}+\frac{b+3c+8+8}{12}+\frac{c+3a+8+8}{12}=\frac{a+b+c}{3}+4=\frac{6}{3}+4=6$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=2$
c. Áp dụng BĐT Cô-si:
\(\text{VT}\leq \frac{9a+a(b+7)}{6}+\frac{9b+b(c+7)}{6}+\frac{9c+c(a+7)}{6}=\frac{16(a+b+c)}{6}+\frac{ab+bc+ac}{6}=16+\frac{ab+bc+ac}{6}\)
Cũng áp dụng BĐT Cô-si:
$ab+bc+ac\leq \frac{(a+b+c)^2}{3}=\frac{6^2}{3}=12$
$\Rightarrow \text{VT}\leq 16+\frac{12}{6}=18$ (đpcm)
Dấu "=" xảy ra khi $a=b=c=2$
d.
Áp dụng BĐT Cô-si:
\(\text{VT}\leq \frac{4a+(b+6)}{4}+\frac{4b+(c+6)}{4}+\frac{4c+(a+6)}{4}=\frac{5(a+b+c)+18}{4}=\frac{30+18}{4}=12\) (đpcm)
Dấu "=" xảy ra khi $a=b=c=2$
e.
Áp dụng BĐT Cô-si:
\(\text{VT}\leq \frac{a+6+8+8}{12}+\frac{b+6+8+8}{12}+\frac{c+6+8+8}{12}=\frac{a+b+c+66}{12}=\frac{6+66}{12}=\frac{72}{12}=6\) (đpcm)
Dấu "=" xảy ra khi $a=b=c=2$

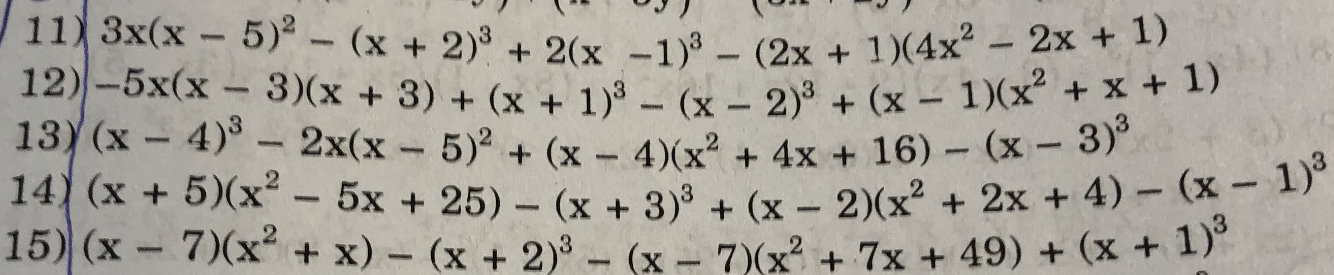
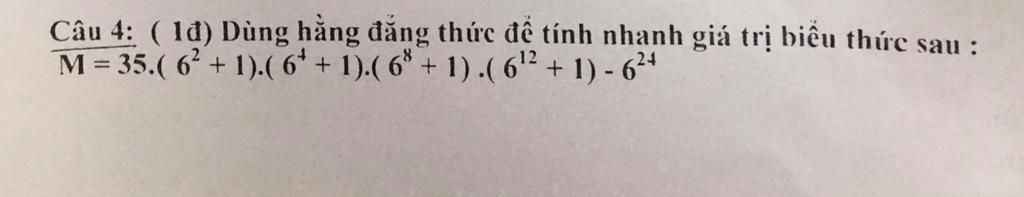
 giúp mik với mn ơi
giúp mik với mn ơi 

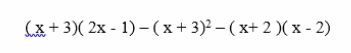
bài 2 a và b