K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
1
8 tháng 7 2023
1: Khi x=64 thì A=7/(8+8)=7/16
2: =(x+3căn x+2căn x-24)/(x-9)=(x+5căn x-24)/(x-9)
\(=\dfrac{\left(\sqrt{x}+8\right)\left(\sqrt{x}-3\right)}{x-9}=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)
28 tháng 7 2021
a) Thay m=-1 vào phương trình, ta được:
\(x^2-2\cdot2x+\left(-1\right)^2+3=0\)
\(\Leftrightarrow x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x=2\)
Thay m=3 vào phương trình, ta được:
\(x^2-2\cdot6x+3^2+3=0\)
\(\Leftrightarrow x^2-12x+12=0\)
\(\text{Δ}=\left(-12\right)^2-4\cdot1\cdot12=144-48=96\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{12-4\sqrt{6}}{2}=6-2\sqrt{6}\\x_2=\dfrac{12+4\sqrt{6}}{2}=6+2\sqrt{6}\end{matrix}\right.\)
c) Ta có: \(\text{Δ}=\left[-2\left(m+3\right)\right]^2-4\left(m^2+3\right)\)
\(=4\left(m^2+6m+9\right)-4\left(m^2+3\right)\)
\(=4m^2+24m+36-4m^2-12\)
\(=24m+24\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
hay m>-1
28 tháng 7 2021
b) Thay x=4 vào phương trình, ta được:
\(4^2-8\left(m+3\right)+m^2+3=0\)
\(\Leftrightarrow m^2+3+16-8m-24=0\)
\(\Leftrightarrow m^2-8m-5=0\)
\(\text{Δ}=\left(-8\right)^2-4\cdot1\cdot\left(-5\right)=64+20=84\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{8-2\sqrt{21}}{2}=4-\sqrt{21}\\m_2=\dfrac{8+2\sqrt{21}}{2}=4+\sqrt{21}\end{matrix}\right.\)
5 tháng 9 2021
Bài 1:
a: Ta có: \(\dfrac{x-2}{5}-1=\dfrac{2x-1}{2}\)
\(\Leftrightarrow2x-4-10=10x-5\)
\(\Leftrightarrow-8x=9\)
hay \(x=-\dfrac{9}{8}\)
5 tháng 9 2021
b: Ta có: \(\dfrac{3}{5-x}=\dfrac{2}{25-x^2}\)
\(\Leftrightarrow3\left(5+x\right)=2\)
\(\Leftrightarrow x=-13\)
c: Ta có: \(x\left(2-x^2\right)+\left(x-2\right)\left(x^2+2x+4\right)>3\)
\(\Leftrightarrow2x-x^3+x^3-8>3\)
\(\Leftrightarrow2x>11\)
hay \(x>\dfrac{11}{2}\)
21 tháng 6 2021
đặt \(A=\sqrt{2-\sqrt{3}}\)
\(=>A.\sqrt{2}=\sqrt{4-2\sqrt{3}}\)
\(A\sqrt{2}=\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}+1}\)
\(A\sqrt{2}=\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(A\sqrt{2}=\sqrt{3}-1=>A=\dfrac{\sqrt{3}-1}{\sqrt{2}}\)
10 tháng 1 2022
Đặt A = 2n + 1 (*)
+) Với n = 1 ta có A = 3 chia hết cho 3
+) Với n > 1 giả sử (*) đúng với n = 2k + 1( k thuộc N ) => 22k+1 + 1 chia hết cho 3
Cần chứng minh (*) đúng với n = 2k + 3
Ta có : A = 2n + 1 = 22k+3 + 1 = 22k+1+2 + 1 = 22k+1.22 + 1
= 4( 22k+1 - 2 ) + 9 = 4( 22k+1 + 1 - 3 ) + 9 = 4.(22k+1 + 1 ) - 3 chia hết cho 3 ( theo giả thiết quy nạp )
Vậy ta có đpcm
Bài giải này nếu có sai sót mong các bạn/anh/chị sửa ạ:v
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
\(n=2k+1\Rightarrow A=2^n+1=2^{2k+1}+1=2.4^k+1\)
Do \(4\equiv1\left(mod3\right)\Rightarrow4^k\equiv1\left(mod3\right)\Rightarrow2.4^k\equiv2\left(mod3\right)\)
\(\Rightarrow2.4^k+1\equiv3\left(mod3\right)\) hay \(2.4^k+1⋮3\Rightarrow A⋮3\)
AH
Akai Haruma
Giáo viên
16 tháng 5 2021
Lời giải:
a) Với $m=3$ thì pt trở thành:
$x^2-6x+4=0$
$\Leftrightarrow (x-3)^2=5$
$\Rightarrow x-3=\pm \sqrt{5}\Rightarrow x=3\pm \sqrt{5}$
b) $(x_1+1)(x_2+1)^2=2$ hay $(x_1+1)(x_2+1)=2$ vậy bạn?
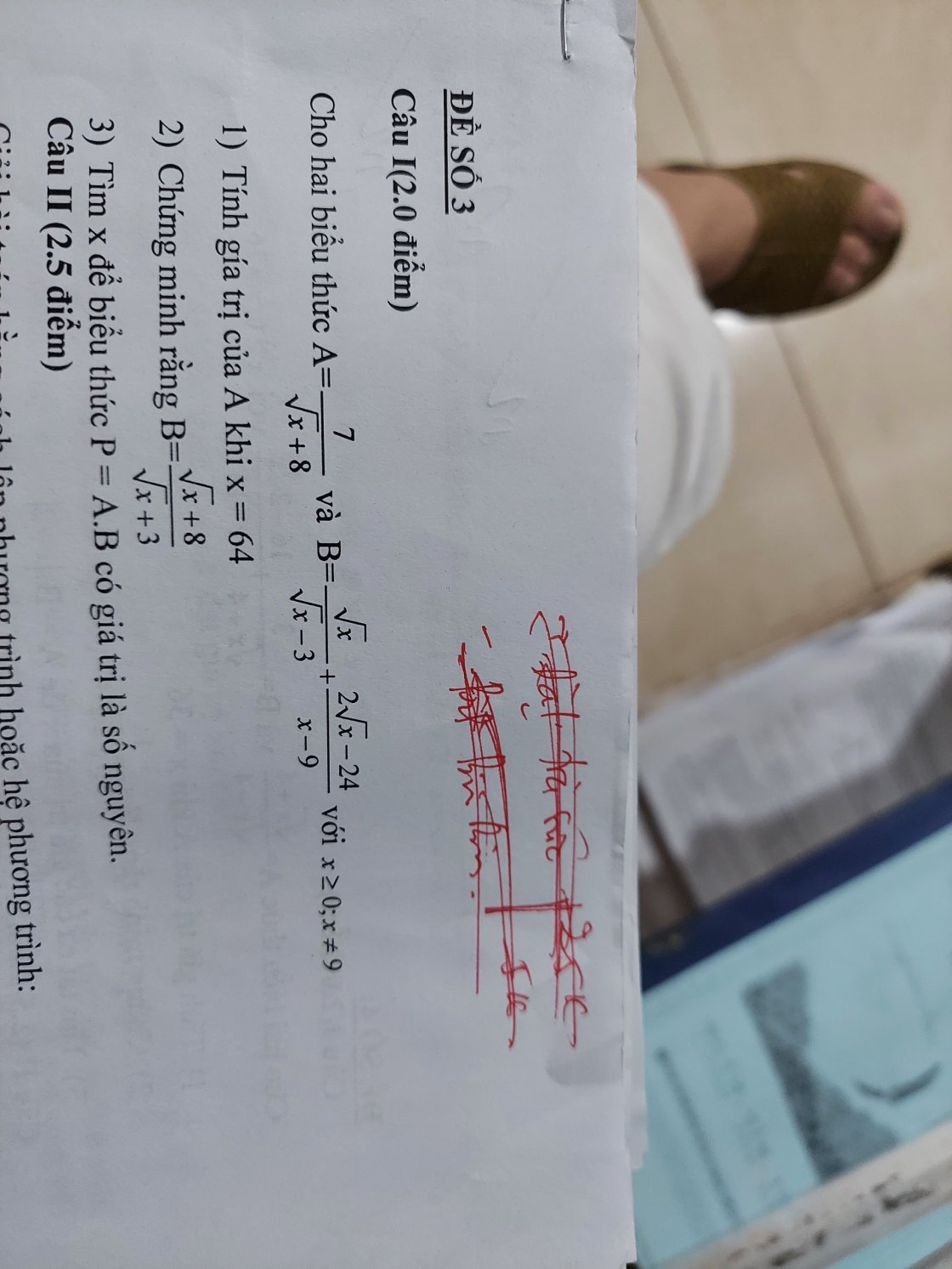
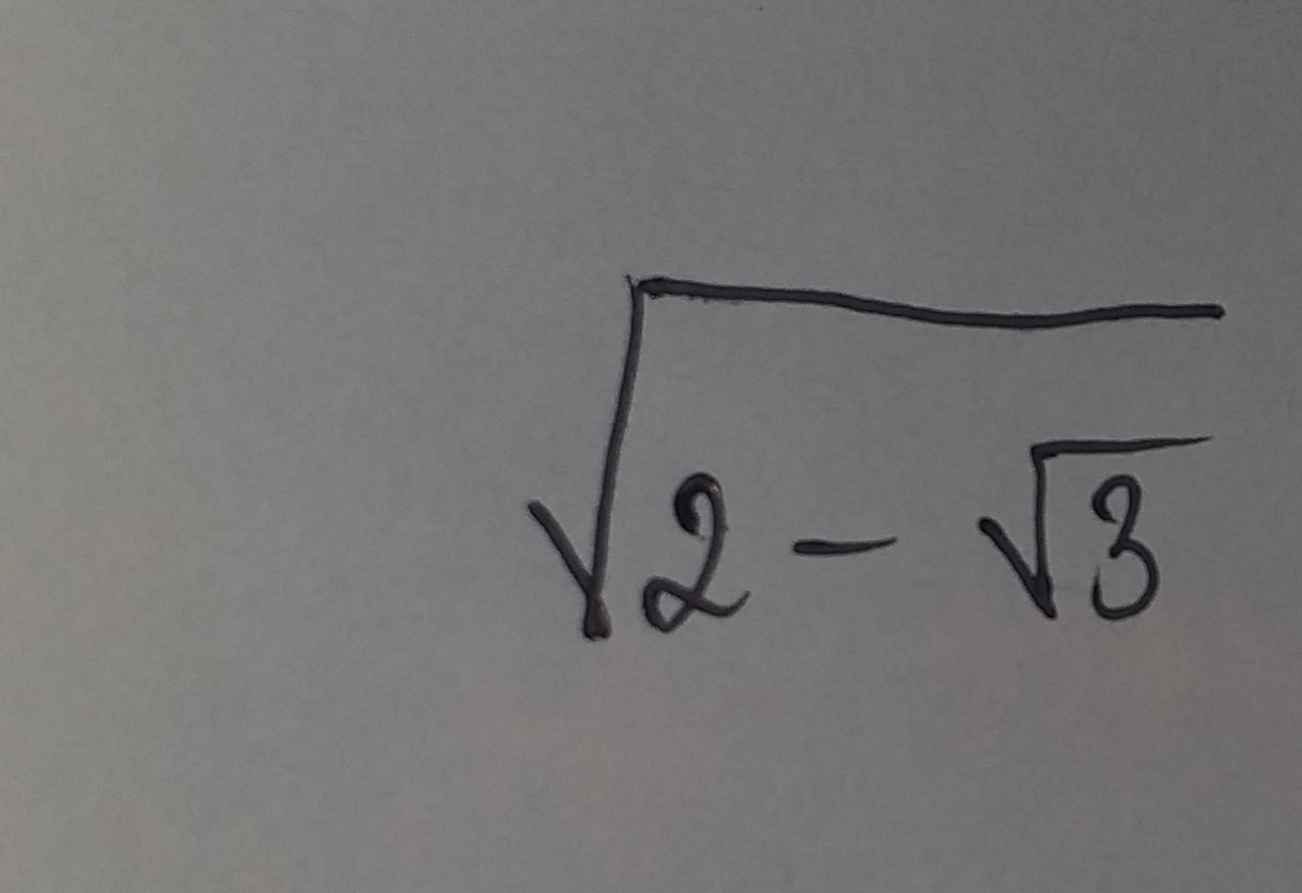
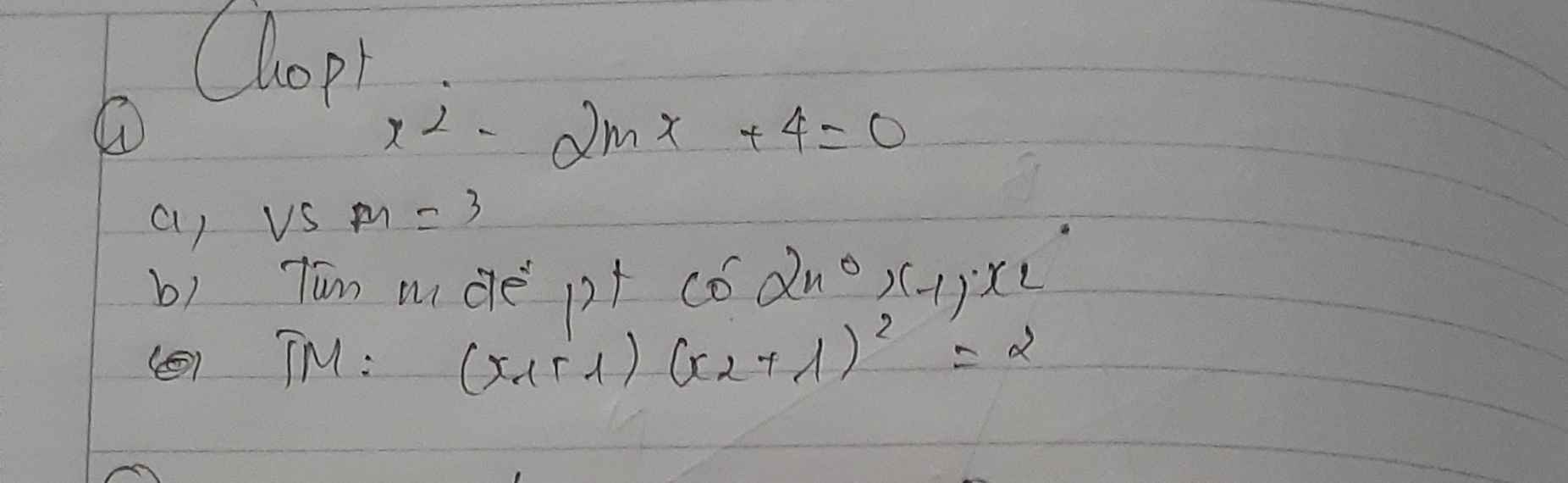
Câu 10: B
Câu 11: A