
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải:
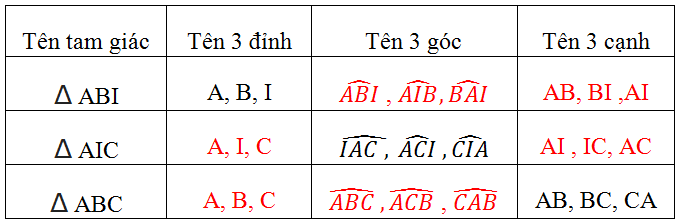
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
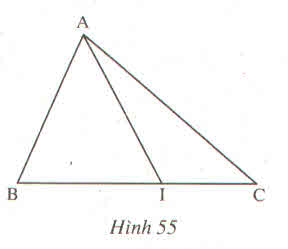
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |

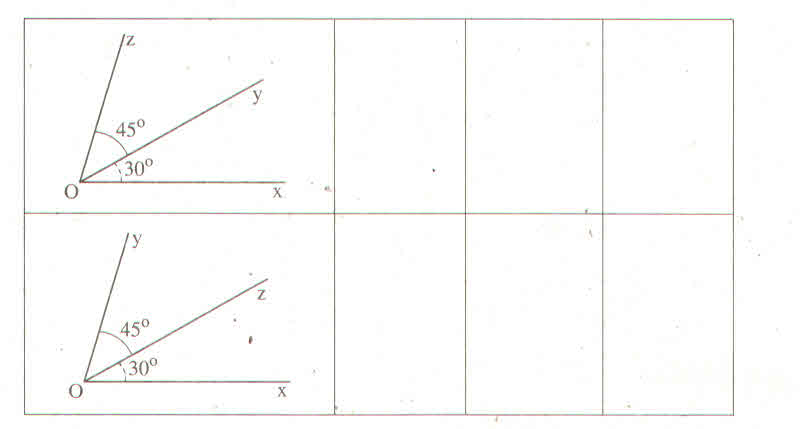
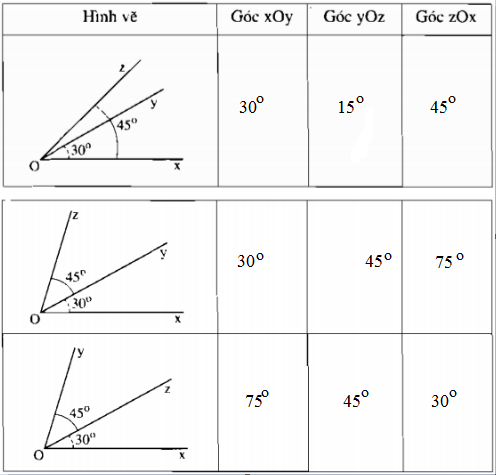
Giải:
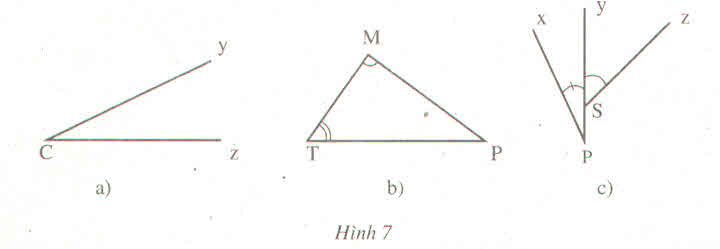
|
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|

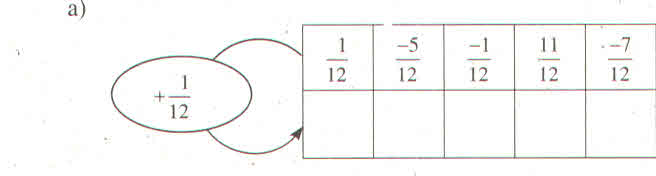
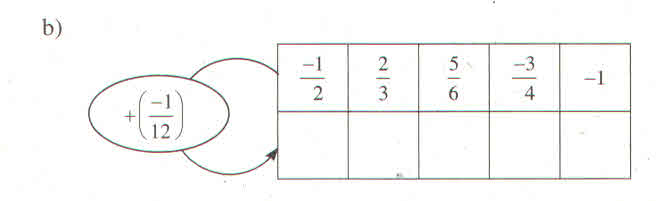
Các kết quả trên đều đúng nên mình điền luôn kết quả nha bạn:
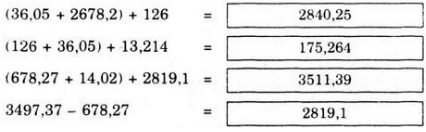
(36,05+2678,2)+126=2840,25.
(126+36,05)+13,214=175,264.
(678,27+14,02)+2819,1=3511,39.
3497,37-678,27=2819,1.
Đó là kết quả của mình có gì sai thì mog pn chỉ ra và giúp mik sửa lỗi nhé!
- Các phép cộng đều cho kết quả đúng.
- Ta có:
(36,05 + 2678,2) + 126
= 36,05 + (2678,2 + 126) (Tính chất kết hợp)
= 36,05 + 2804,2 (theo a)
= 2840,25 (theo c)
(126 + 36,05) + 13,214
= 126 + (36,05 + 13,214) (tính chất kết hợp)
= 126 + 49,264 (theo b)
= 175,264 (theo d)
(678,27 + 14,02) + 2819,1
= (678,27 + 2819,1) + 14,02 (Tính chất giao hoán và kết hợp)
= 3497,37 + 14,02 (theo e)
= 3511,39 (theo g)
3497,37 – 678,27 = 2819,1 (suy từ e)
Vì vậy ta có thể điền số thích hợp và ô trống mà không cần tính toán:


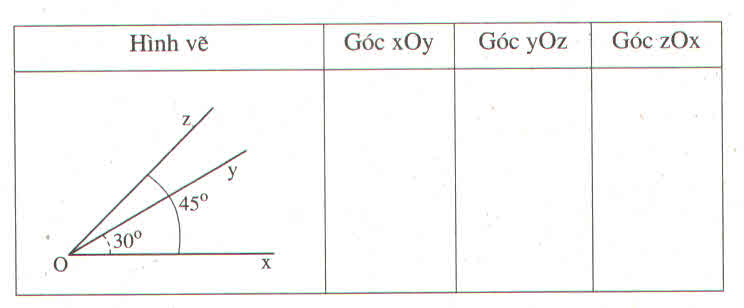
Số nguyên biểu thị điểm:
- Điểm N: 2
- Điểm P: -3
- Điểm Q: -5
Số nguyên biểu thị điểm:
- Điểm N : 2
- Điểm P : -3
- Điểm Q : -5
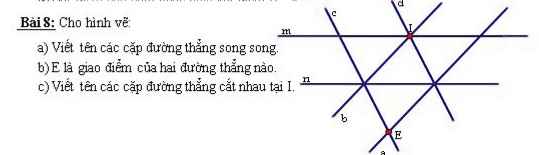













a: m//n
c//d
b//a
b:E là giao điểm của a và c
c: Các đường thẳng giao nhau tại I là d,m,b