
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tý cần phải lấy ít nhất 4 chiếc vì sẽ có nhiều nhất 3 chiếc khác nhau

\(\Leftrightarrow\left\{{}\begin{matrix}8x-20y=44\\15x+20y=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)

giả sử phương trình đã cho có nghiệm này gấp đôi nghiệm kia
Và áp dụng hệ thúc viet ta có:
\(\begin{cases}x_1+x_2=-p\\x_{1.}.x_2=q\\x_1=2x_2\end{cases}\)=>\(\begin{cases}2x_2+x_2=-p\\x_{1.}.x_2=q\\x_1=2x_2\end{cases}\)=>\(\begin{cases}3x_2=-p\\x_{1.}.x_2=q\\x_1=2x_2\end{cases}\)=>\(\begin{cases}x_2=\frac{-p}{3}\\x_{1.}.x_2=q\left(1\right)\\x_1=\frac{-2p}{3}\end{cases}\)
Thay \(x_1\)=\(\frac{-2p}{3}\); \(x_2\)=\(\frac{-p}{3}\) vào (1) ta có:
\(\frac{-2p}{3}\).\(\frac{-p}{3}\)=q
2\(p^2\)=9q
2\(p^2\)-9q=0
Vậy khi 2\(p^2\)-9q=0 thì phương trình trên có nghiệm này gấp 2 nghiệm kia

\(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\left[\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x^3}-1}-\dfrac{x+\sqrt{x}+1}{\sqrt{x^3}-1}\right]:\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\left(\dfrac{x+2+x-\sqrt{x}+2\sqrt{x}-2-x-\sqrt{x}-1}{\sqrt{x^3}-1}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\)
\(=1\)
\(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right).\dfrac{1}{2a\sqrt{a}}\)
\(=\left[\dfrac{\left(\sqrt{a}+1\right)^2}{a-1}-\dfrac{\left(\sqrt{a}-1\right)^2}{a-1}+\dfrac{4\sqrt{a}\left(a-1\right)}{a-1}\right].\dfrac{1}{2a\sqrt{a}}\)
\(=\left(\dfrac{a+2\sqrt{a}+1-a+2\sqrt{a}-1+4a\sqrt{a}-4\sqrt{a}}{a-1}\right).\dfrac{1}{2a\sqrt{a}}\)
\(=\dfrac{4a\sqrt{a}}{a-1}.\dfrac{1}{2a\sqrt{a}}\)
\(=\dfrac{2}{a-1}\)

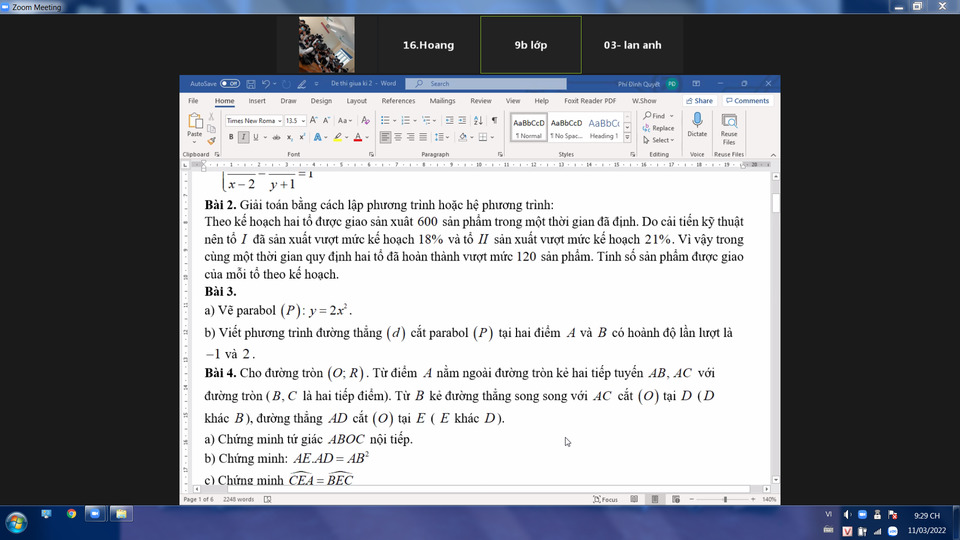
BÀi 4
a) Ta có góc OBA= góc OCA =90 độ ( tính chất tiếp tuyến)
=> ABOC nội tiếp
b) Xét tam giác ABE và ADB có
góc BAD chung
góc ABE= góc ADB(=1/2 sđ cung BE)
=> Tam giác ABE đồng dạng tam giác ADB
=>\(\dfrac{AB}{AD}=\dfrac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Ta có BD//AC
=> góc BDE= góc EAC(slt)
mak góc BDE= góc BCE(=1/2 sđ cung BE)
=> góc BCE= góc EAC
Mặt khác ta lại có góc CBE= góc ECA(=1/2 sđ cung EC)
=> tam giác BEC đồng dạng tam giác CEA
=> góc CEA = góc BEC
Bài 3
Gọi pt đường thẳng (d) là y=ax+b
ta có (d) cắt (P) tại 2 điểm có hoành độ là -1 và 2
=> \(\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Thay vào (P) ta được
\(\Rightarrow\left[{}\begin{matrix}x=-1\Rightarrow y=2\\x=2\Rightarrow y=8\end{matrix}\right.\)
để (d) cắt (P) tại 2 điểm ta có hệ pt\(\Rightarrow\left\{{}\begin{matrix}-a+b=2\\2a+b=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=2\\b=4\end{matrix}\right.\)
Vậy Pt đường thẳng (d) là y=2x+4



1. 3x2 - 2x = 0 <=> x.(3x - 2) = 0 <=> x = 0 hoặc x = 2/3
2. 2x2 - 10 = 0 <=> 2x2 = 10 <=> x = √5 hoặc x = -√5
3. x2 - 49 = 0 <=> x2 = 49 <=> x = 7 hoặc x = -7
4. x2 - 7x + 6 = 0 <=> x2 - 6x - x + 6 = 0 <=> x.(x - 6) - (x - 6) = 0 <=> (x - 1).(x - 6) = 0 <=> x = 1 hoặc x = 6
5. 4x2 - 3x - 2 = 0. Có: a = 4, b = -3, c = -2 với a, b, c là hệ số của phương trình. Có: △ = b2 - 4ac = 9 - 4.(-2).4 = 41. Do △ > 0 nên phương trình sẽ có hai nghiệm:
x1 = \(\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3-\sqrt{41}}{8}\)
x2 = \(\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+\sqrt{41}}{8}\)


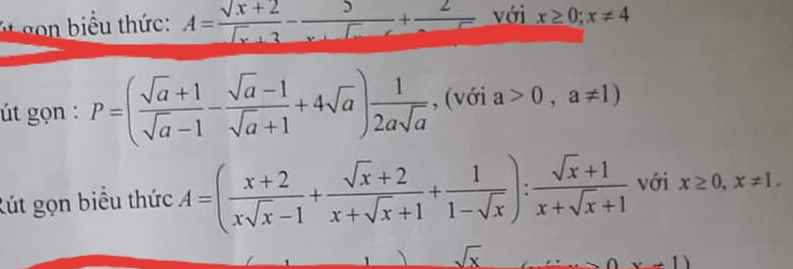


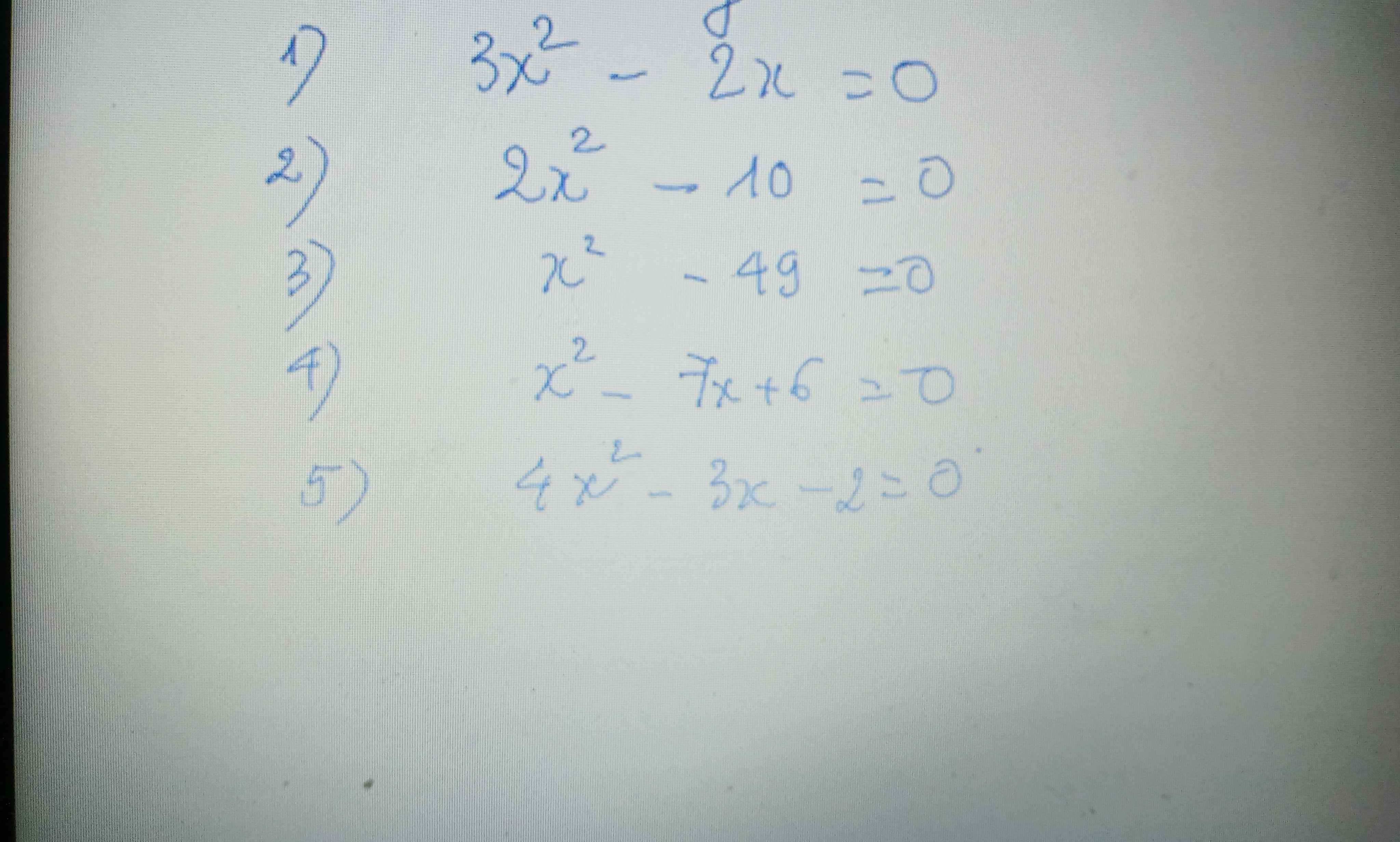

Câu b là \(\widehat{CFD}=\widehat{DCB}\) hay \(\widehat{CFD}=\widehat{OCB}\) vậy nhỉ? Em viết chữ D với O giống nhau quá ko biết là chữ nào