
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có gì ko hiểu bạn hỏi nhé
\(|2x+1|-|x-1|=3x\left(1\right)\)
Ta có:
\(2x+1=0\Leftrightarrow x=\frac{-1}{2}\)
\(x-1=0\Leftrightarrow x=1\)
Lập bảng xét dấu :
2x+1 x-1 -1/2 1 -0 0 0 - - - + + + +
+) Với \(x< \frac{-1}{2}\Rightarrow\hept{\begin{cases}2x+1< 0\\x-1< 0\end{cases}\Rightarrow}\hept{\begin{cases}|2x+1|=-2x-1\\|x-1|=1-x\end{cases}\left(2\right)}\)
Thay (2) vào (1) ta được :
\(\left(-2x-1\right)-\left(1-x\right)=3x\)
\(-2x-1-1+x=3x\)
\(-2x+x-3x=1+1\)
\(-4x=2\)
\(x=\frac{-1}{2}\)( loại )
+) Với \(\frac{-1}{2}\le x< 1\Rightarrow\hept{\begin{cases}2x+1>0\\x-1< 0\end{cases}\Rightarrow\hept{\begin{cases}|2x+1|=2x+1\\|x-1|=1-x\end{cases}\left(3\right)}}\)
Thay (3) vào (1) ta được :
\(\left(2x+1\right)-\left(1-x\right)=3x\)
\(2x+1-1+x=3x\)
\(3x=3x\)( luôn đúng chọn )
+) Với \(x\ge1\Rightarrow\hept{\begin{cases}2x+1>0\\x-1>0\end{cases}\Rightarrow\hept{\begin{cases}|2x+1|=2x+1\\|x-1|=x-1\end{cases}\left(4\right)}}\)
Thay (4) vào (1) ta được :
\(\left(2x+1\right)-\left(x-1\right)=3x\)
\(2x+1-x+1=3x\)
\(2x-x-3x=-1-1\)
\(-2x=-2\)
\(x=1\)( chọn )
Vậy \(\frac{-1}{2}\le x\le1\)
\(\left|2x+1\right|-\left|x-1\right|=3x\Rightarrow\left|2x+1-1+x\right|\ge3x\)
\(\Leftrightarrow\left|3x\right|\ge3x\Rightarrow x\in\left\{x\inℤ|x\le0\right\}\)


Hello mình 2k6 nè kết bn nhé !!!!
Vào đây nè !!!
https://loga.vn/bai-viet/on-tap-chung-minh-hai-duong-thang-song-song-3945

\(\widehat{B_2}=\widehat{B_4}=60^0\left(đối.đỉnh\right)\\ \widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{B_1}=180^0-60^0=120^0\\ \Rightarrow\widehat{B_3}=\widehat{B_1}=120^0\left(đối.đỉnh\right)\)
Vì a//b nên \(\widehat{B_2}=\widehat{A_4}=60^0;\widehat{B_1}=\widehat{A_3}=120^0\left(so.le.trong\right)\)
Ta có \(\left\{{}\begin{matrix}\widehat{A_2}=\widehat{A_4}=60^0\\\widehat{A_1}=\widehat{A_3}=120^0\end{matrix}\right.\left(đối.đỉnh\right)\)

12:
1: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
2: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
3: ΔBCF cân tại B
mà BD là phân giác
nên BD vuông góc CF

`(x-1/3)^2=25/36`
`=> (x-1/3)^2 =(5/6)^2`
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{5}{6}\\x-\dfrac{1}{3}=-\dfrac{5}{6}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{6}+\dfrac{1}{3}\\x=-\dfrac{5}{6}+\dfrac{1}{3}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{6}+\dfrac{2}{6}\\x=-\dfrac{5}{6}+\dfrac{2}{6}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{6}\\x=-\dfrac{3}{6}=-\dfrac{1}{2}\end{matrix}\right.\)



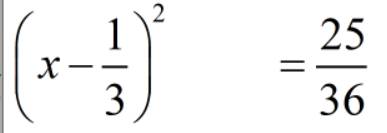
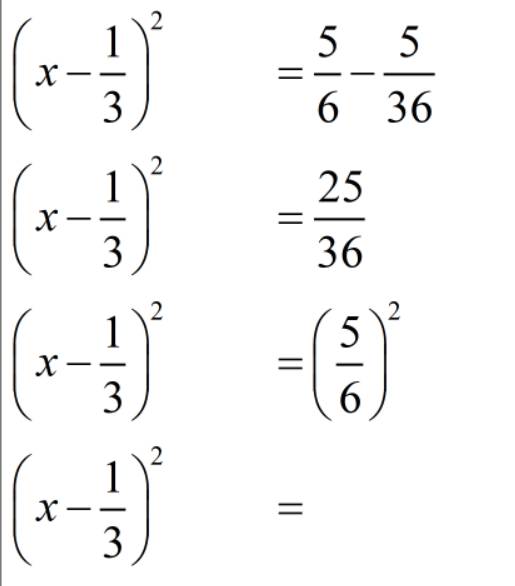 như vầy mà ko biết làm nx,bạn nào biết thì chỉ tui nha!!!
như vầy mà ko biết làm nx,bạn nào biết thì chỉ tui nha!!!
a: k=-2
b: y=-2x