
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 4:
a: Xét ΔIAM và ΔIEB có
góc IAM=góc IEB
IE=IA
góc AIM=góc EIB
Do đo: ΔIAM=ΔIEB
=>AM=BE
b: ΔAIM=ΔEIB
=>IB=IM
=>I là trung điểm của BM
Xét tứ giác ANEC có
I là trung điểm chung của AE và NC
nên ANEC là hình bình hành
=>AN//EC
Xét tứ giác AMEB có
I là trung điểm chung của AE và MB
nên AMEB là hình bình hành
=>AM//BE
mà AN//BE
nên M,A,N thẳng hàng


Bài 1. Điền kí hiệu ( ∈,⊂, ∉) thích hợp vào ô vuông
– 3 ∉ N – 3 ∈ Z -3 ∈ Q
-2/3 ∉ Z -2/3 ∈ Q N ⊂ Z ⊂ Q
Bài 2 trang 7. Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ 3/-4

bài 3
hD Giải: a) x= 2/-7 = -22/7;y = -3/11= -21/77
Vì -22 < -21 và 77> 0 nên x <y
b)![]() Vì -216 < -213 và 300 > 0 nên y < x
Vì -216 < -213 và 300 > 0 nên y < x
c) x = -0,75 = -75/100 = -3/4; y = -3/4
Vậy x=y
Bài 4. So sánh số hữu tỉ a/b ( a,b ∈ Z, b # 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu
HD giải: Với a, b ∈ Z, b> 0
– Khi a , b cùng dấu thì a/b > 0
– Khi a,b khác dấu thì a/b < 0
Tổng quát: Số hữu tỉ a/b ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0

Câu 3:
a: Xét ΔABC có AB<BC
nên \(\widehat{ACB}< \widehat{BAC}\)
b: Xét ΔABM có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABM cân tại A
mà \(\widehat{B}=60^0\)
nên ΔABM đều


Câu 9:
Thời gian muộn nhất để bố đi vào sân bay là:
3h30'-2h-30'=1h(chiều)

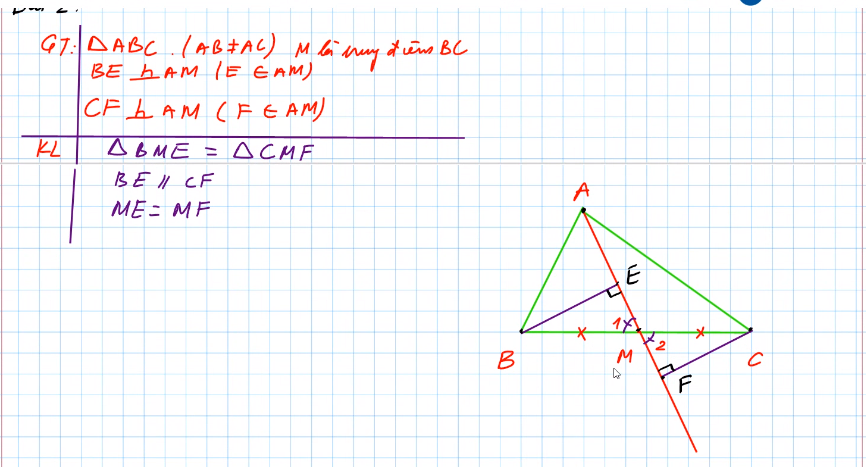
a: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó: ΔBME=ΔCMF
Suy ra: ME=MF
b: Xét tứ giác BECF có
M là trung điểm của BC
M là trung điểm của FE
Do đó: BECF là hình bình hành
Suy ra: BE//CF

b) Ta có: \(\left|2x-1\right|=\left|x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+3\\2x-1=-x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=3+1\\2x+x=-3+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{2}{3}\end{matrix}\right.\)







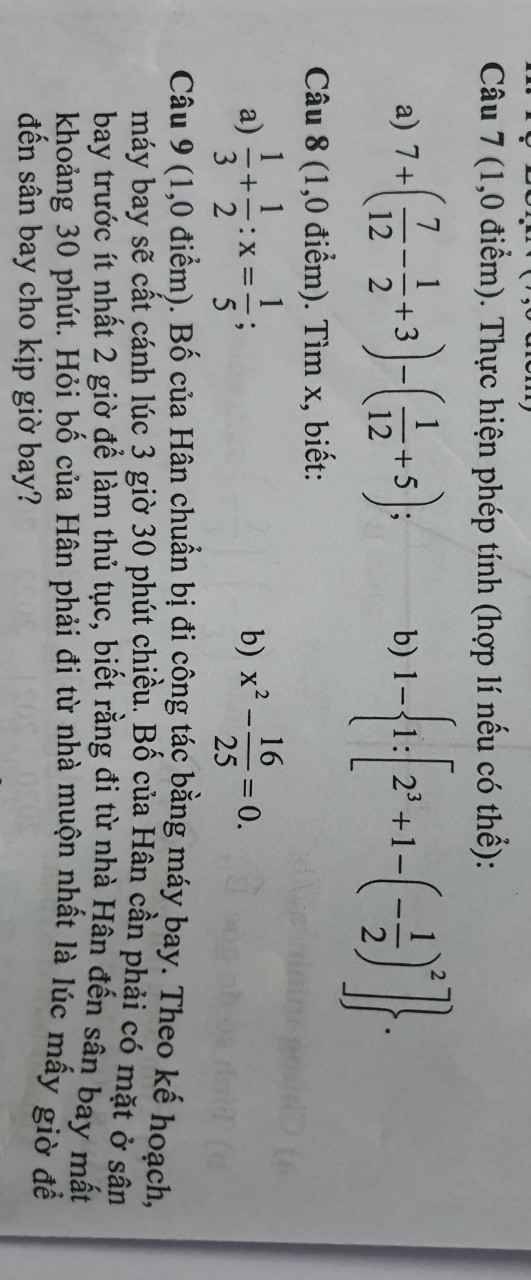 giúp tui bài 9
giúp tui bài 9
 giúp tui bài 3 gấp lắm
giúp tui bài 3 gấp lắm