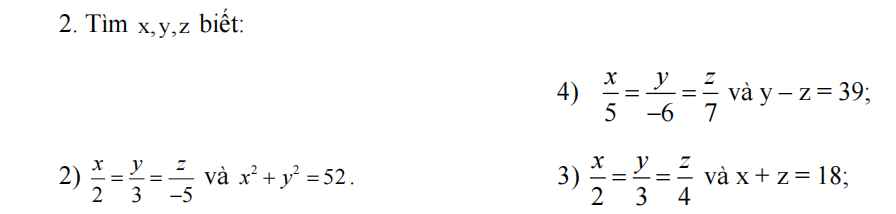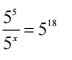Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Đặt \(\dfrac{a}{c}=\dfrac{c}{b}=k\)
\(k^2=\dfrac{a}{c}.\dfrac{c}{b}=\dfrac{a}{b}\) (1)
\(k^2=\dfrac{a^2}{c^2}=\dfrac{c^2}{b^2}=\dfrac{a^2+c^2}{b^2+c^2}\) ( t/c dãy tỉ số bằng nhau )
Từ (1), (2) \(\Rightarrow\dfrac{a^2+c^2}{b^2+c^2}=\dfrac{a}{b}\left(đpcm\right)\)
Ta có \(\dfrac{a}{c}\)= \(\dfrac{c}{b}\) => \(\dfrac{a^2}{c^2}\) = \(\dfrac{c^2}{b^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{a^2}{c^2}\) = \(\dfrac{c^2}{b^2}\) = \(\dfrac{a^2+c^2}{b^2+c^2}\) (1)
Ta có \(\dfrac{a^2}{c^2}\) = \(\dfrac{a.a}{c.c}\) = \(\dfrac{a.c}{c.b}\)=\(\dfrac{a}{b}\) (vì \(\dfrac{a}{c}\)=\(\dfrac{c}{b}\)) (2)
Từ (1)(2) => \(\dfrac{a^2+c^2}{b^2+c^2}\) = \(\dfrac{a}{b}\) (đpcm)

B2 = A2 ( Vì B2 và A2 là đồng vị )
Nên A2 = B2 = 1200
B1+ B2 = 180o = 180 - B2 = 180 - 120 = 60o
A4 = B2 = 120o ( goc sole trong )
B1 = A3 = 120o ( goc1 sole trong )

3: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+z}{2+4}=\dfrac{18}{6}=3\)
Do đó: x=6; y=9; z=12

4. Tam giác ABC = Tam giác MNP (gt).
=> \(\left\{{}\begin{matrix}\text{^B = ^N (2 cặp góc tương ứng).}\\\text{^A = ^M (2 cặp góc tương ứng).}\end{matrix}\right.\)
Mà ^A = 80o (gt).
=> ^M = 80o.
Tam giác ABC = Tam giác MNP (gt).
=> ^C = ^P (2 cặp góc tương ứng).
Mà ^P = 45o (gt).
=> ^C = 45o.
Xét tam giác ABC có: ^A + ^B + ^C = 180o ( Tổng 3 góc trong 1 tam giác).
Mà ^A = 80o (gt).
^C = 45o (cmt).
=> ^B = 55o.
Mà ^B = ^N (cmt).
=> ^N = 55o.

Lời giải:
$\frac{5^5}{5^x}=5^{18}$
$5^{5-x}=5^{18}$
$5-x=18$
$x=-13$

bạn làm mik thấy hợp lí
tui sắp thi Toán rồi ,chắc tui ngất qá ![]()

132;142;152;124;134;154;214;234;254;312;314;342;324;354;352;412;432;452;512;514;524;542;532;534
Vậy có 24 số
À bạn ơi số có 3 chữ số khác nhau hay giống nhau vậy bạn
cả khác nhau cả giống nhau bn ^^
à mà... bài này là tìm số các số chứ k phải liệt kê các số !
hình như kết quả là 50 số đó !

ban a neu muon nguoi ta ket ban phai hoi truc tiep ten nguoi ta da ban khong duoc hoi linh tinh tren trang hoi dap cua onine math dau lam nhu vay la trai luat day co the ban se bi khoa trang hoi dap day can than nhe chao ban