Giúp tôi với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 5 2023
a: Thay x=0 và y=5 vào (d), ta được:
m*0+5=5
=>5=5(đúng)
=>ĐPCM
b: x1<x2; |x1|>|x2|
=>x1*x2<0
PTHĐGĐ là:
x^2-mx-5=0
Vì a*c<0
nên x1,x2 luôn trái dấu
=>Với mọi m
25 tháng 6 2023
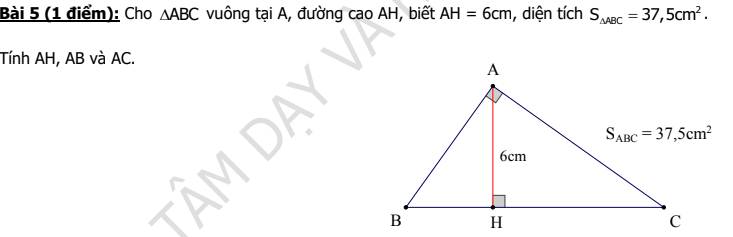
BC=2*37,5:6=75:6=12,5cm
Đặt HB=x; HC=y(x<y)
Theo đề, ta có: x+y=12,5 và xy=36
Do đó: x,y là các nghiệm của pt là:
a^2-12,5a+36=0
=>a=4,5 hoặc a=8
=>BH=4,5; CH=8
AB=căn 4,5*12,5=7,5cm
AC=căn 8*12,5=10cm
25 tháng 10 2021
Bài 5:
Thay x=1 và y=5 vào (d), ta được:
b+2=5
hay b=3
13 tháng 5 2021
Bài 2:
a) Ta có: \(\text{Δ}=\left(m+1\right)^2-4\left(m-5\right)\)
\(=m^2+2m+1-4m+20\)
\(=m^2-2m+1+20\)
\(=\left(m-1\right)^2+20>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt với mọi m
KA
3
SB
giúp tôi check đáp án câu này với
1
28 tháng 9 2021
\(3x-2\sqrt{3x-2}=1\left(đk:x\ge\dfrac{2}{3}\right)\)
\(\Leftrightarrow2\sqrt{3x-2}=3x-1\)
\(\Leftrightarrow4\left(3x-2\right)=9x^2-6x+1\)
\(\Leftrightarrow9x^2-18x+9=0\)
\(\Leftrightarrow9\left(x-1\right)^2=0\Leftrightarrow x=1\left(tm\right)\)
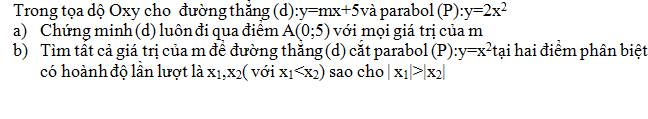
a, Gọi pt đường thẳng AB có dạng y = ax + b
pt đường thẳng đi qua A(1;-1) <=> a + b = -1
pt đường thẳng đi qua B(5;7) <=> 5a + b = 7
Ta có hệ : \(\hept{\begin{cases}a+b=-1\\5a+b=7\end{cases}}\Leftrightarrow\hept{\begin{cases}-4a=-8\\b=-1-a\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=-3\end{cases}}\)
Vậy pt đường thẳng AB có dạng : 2x - 3 = y
b, (d) cắt đường thẳng AB tại 1 điểm trục Oy => tọa độ điểm đó là (0;-3)
Thay vào (d) ta được : \(-3=2m-9\Leftrightarrow2m-6=0\Leftrightarrow m=3\)