
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

14 tháng 5 2023
a: Thay x=0 và y=5 vào (d), ta được:
m*0+5=5
=>5=5(đúng)
=>ĐPCM
b: x1<x2; |x1|>|x2|
=>x1*x2<0
PTHĐGĐ là:
x^2-mx-5=0
Vì a*c<0
nên x1,x2 luôn trái dấu
=>Với mọi m


13 tháng 5 2021
Bài 2:
a) Ta có: \(\text{Δ}=\left(m+1\right)^2-4\left(m-5\right)\)
\(=m^2+2m+1-4m+20\)
\(=m^2-2m+1+20\)
\(=\left(m-1\right)^2+20>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt với mọi m

29 tháng 10 2021
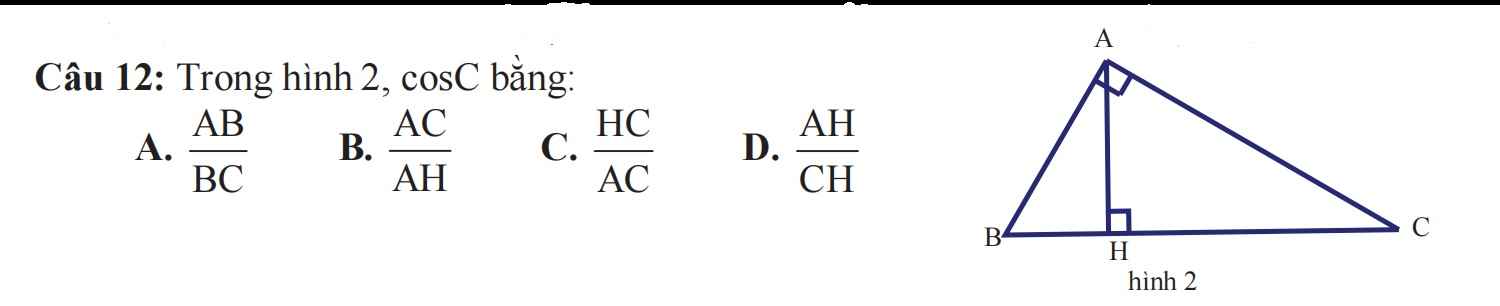
12C (cos = cạnh kề/ cạnh huyền)
13 D (tan = cạnh đối/ cạnh kề)
T
0

T
0


NM
0

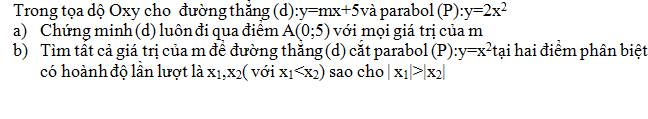


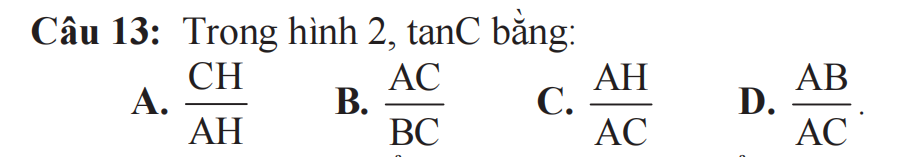



Ptr đâu em?