
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
2: ΔABD đồng dạng với ΔDAC
=>BD/AC=AB/DA=AD/DC
=>AD/16=BD/AC=18/DA
=>AD^2=16*18=288
=>AD=12căn 2(cm)
AC=căn AD^2+DC^2=4căn 82(cm)

CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)


a: BC=căn 6^2+8^2=10cm
bD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
=>BH/BA=BA/BC
=>BH*BC=BA^2
c: Xét ΔBHA có BI là phân giác
nên IH/IA=BH/BA
=>IH/IA=BA/BC=AD/DC



\(A=\left(a^4-2a^3+a^2\right)+\left(a^2-2a+1\right)+1\)
\(A=\left(a^2-a\right)^2+\left(a-1\right)^2+1\ge1\)
\(A_{min}=1\) khi \(\left\{{}\begin{matrix}a^2-a=0\\a-1=0\end{matrix}\right.\) \(\Rightarrow a=1\)

Bài 1:
a) \(=10x\left(x+y\right)+5\left(x+y\right)=5\left(x+y\right)\left(2x+1\right)\)
b) \(=a\left(5y+x\right)-3b\left(5y+x\right)=\left(5y+z\right)\left(a-3b\right)\)
c) \(=x^2\left(x+1\right)-\left(x+1\right)=\left(x+1\right)\left(x^2-1\right)\)
\(=\left(x+1\right)\left(x+1\right)\left(x-1\right)=\left(x+1\right)^2\left(x-1\right)\)
Bài 2:
a) \(\Rightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b) \(\Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x^2+1\right)=0\)
\(\Rightarrow x=-1\)(do \(x^2+1>0\))
c) K hiểu đề lắm
d) \(\Rightarrow2x\left(3x-5\right)+2\left(3x-5\right)=0\)
\(\Rightarrow2\left(3x-5\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-1\end{matrix}\right.\)





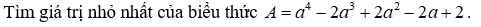


Bài 3:
Ta có: \(\left(x-2\right)\left(x^2+2x+4\right)-x\left(x^2-4\right)=10\)
\(\Leftrightarrow x^3-8-x^3+4x=10\)
\(\Leftrightarrow4x=18\)
hay \(x=\dfrac{9}{2}\)