K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 10 2021
Bài 5:
Thay x=1 và y=5 vào (d), ta được:
b+2=5
hay b=3
23 tháng 10 2021
Câu 1:
a: \(2\sqrt{9}+6\sqrt{4}-3\sqrt{25}\)
\(=2\cdot3+6\cdot2-3\cdot5\)
\(=6+12-15=3\)
b: \(\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\sqrt{3}-\sqrt{2}-\sqrt{3}-\sqrt{2}\)
\(=-2\sqrt{2}\)
9 tháng 11 2021
9) We have CE = BC - BE = x - y
In \(\Delta ABC\), we have \(E\in BC\), \(D\in AB\)and ED//CA, so: \(\frac{AD}{BD}=\frac{CE}{BE}\)(Thales' theorem)
\(\Rightarrow\frac{b}{a}=\frac{x-y}{y}=\frac{x}{y}-1\)\(\Rightarrow b=a\left(\frac{x}{y}-1\right)=\frac{ax}{y}-a\)
So we choose A as the right answer.
19 tháng 3 2021
a) Thay m=1 vào hệ pt, ta được:
\(\left\{{}\begin{matrix}3x-y=1\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-y=1\\3x+6y=15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-7y=-14\\3x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\3x=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất là (x,y)=(1;2)
LV
16
14 tháng 5 2023
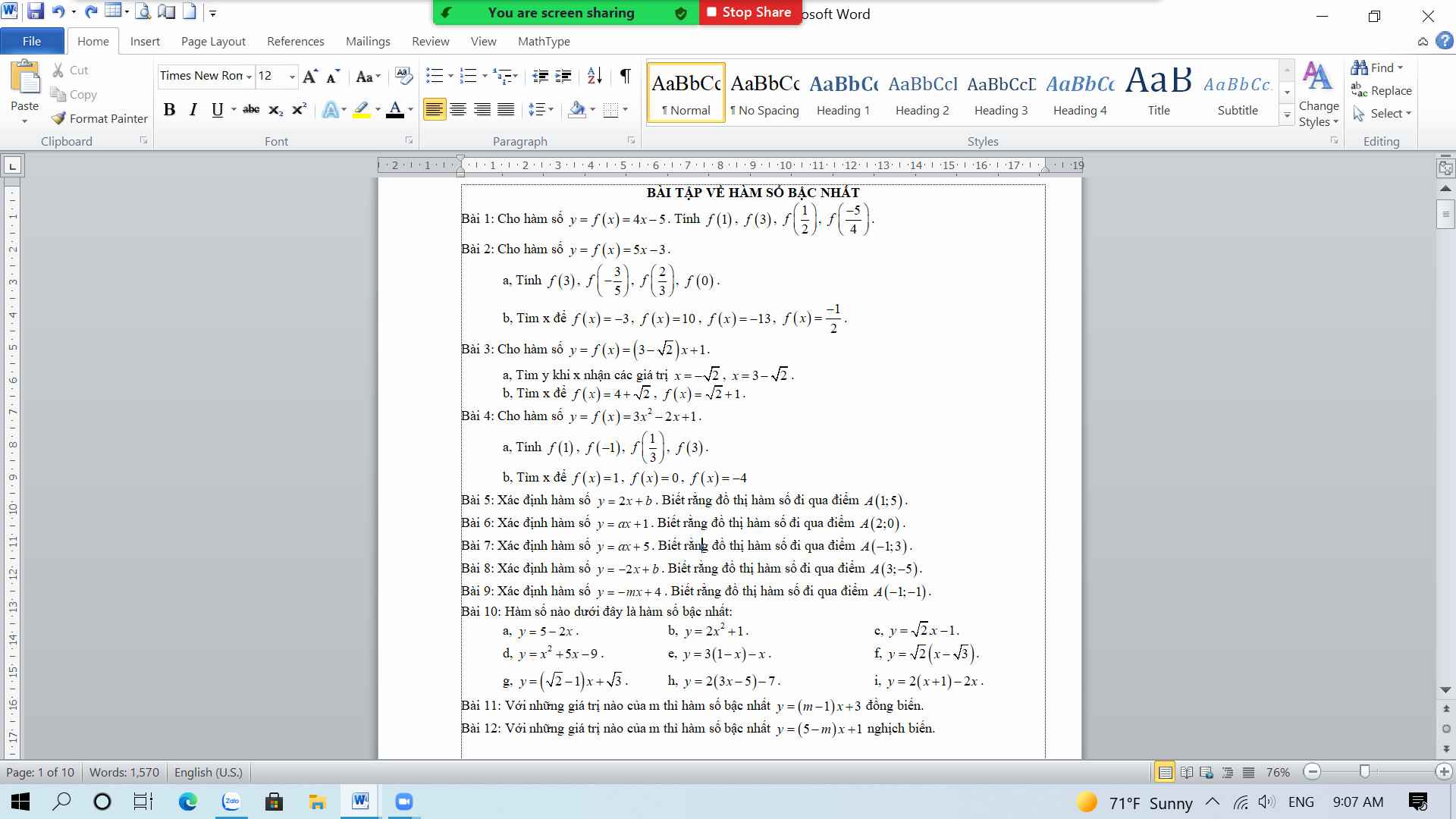
a: Thay x=0 và y=5 vào (d), ta được:
m*0+5=5
=>5=5(đúng)
=>ĐPCM
b: x1<x2; |x1|>|x2|
=>x1*x2<0
PTHĐGĐ là:
x^2-mx-5=0
Vì a*c<0
nên x1,x2 luôn trái dấu
=>Với mọi m
Phương trình ax2 + bx + c = 0 vô nghiệm => Δ = b2 - 4ac > 0 (1)
Xét phương trình ax2 - bx + c = 0 có Δ = (-b)2 - 4ac = b2 - 4ac > 0 [ theo (1) ]
=> Phương trình ax2 - bc + c = 0 vô nghiệm => Chọn D