Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5:
a: ΔABC cân tại A
mà AH là trung tuyến
nên AH vuông góc BC
BH=CH=4cm
=>AH=căn 10^2-4^2=2*căn 21(cm)
b: Xét ΔIBH và ΔIAD có
góc IBH=góc IAD
IB=IA
góc BIH=góc AID
=>ΔIBH=ΔIAD
=>AD=BH=HC

a) Xét tam giâc ABC
có: AB< AC ( 4 cm < 6 cm)
=> góc ACB < góc góc ABC ( quan hệ cạnh với góc đối diện)
b) Xét tam giác ABM vuông tại A và tam giác CDM vuông tại C
có: AM = CM ( gt)
góc AMB = góc CMD ( đối đỉnh)
\(\Rightarrow\Delta ABM=\Delta CDM\left(cgv-gn\right)\)
c) ta có: \(AM=CM=\frac{AC}{2}=\frac{6}{2}=3cm\)
\(\Rightarrow AM=CM=3cm\)
Xét tam giác ABM vuông tại A
có: \(AB^2+AM^2=BM^2\left(py-ta-go\right)\)
thay số: \(4^2+3^2=BM^2\)
\(BM^2=25\)
\(\Rightarrow BM=5cm\)
Xét tam giác ABC
có: BN = CN (gt)
=> AN là đường trung tuyến của BC
có: AM = CM (gt)
=> BM là đường trung tuyến của AC
mà AN cắt BM tại G
=> G là trọng tâm của\(\Delta ABC\)( định lí)
\(\Rightarrow\frac{GM}{BM}=\frac{1}{3}\)( định lí)
thay số: \(\frac{GM}{5}=\frac{1}{3}\Leftrightarrow GM=\frac{1}{3}.5=\frac{5}{3}cm\)
\(\Rightarrow GM=\frac{5}{3}cm\)

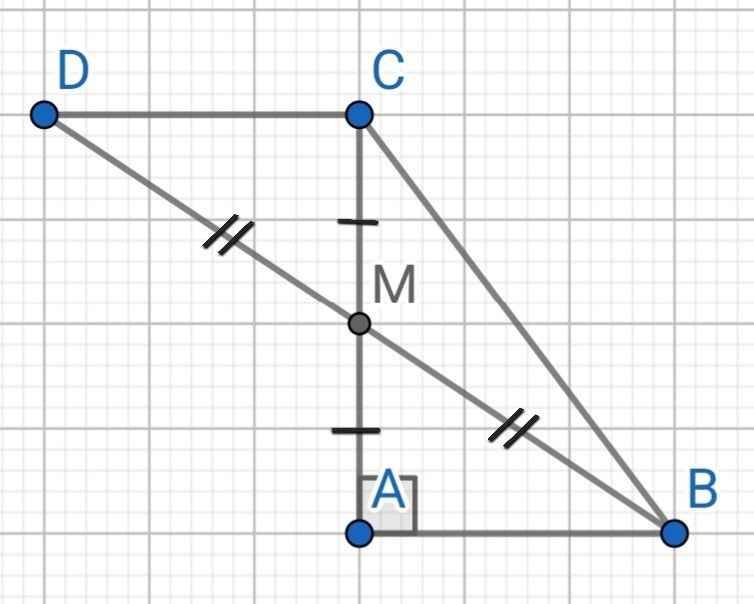 a) Xét ∆ABM và ∆CDM có:
a) Xét ∆ABM và ∆CDM có:
AM = CM (gt)
AMB = CMD (đối đỉnh)
BM = DM (gt)
⇒ ∆ABM = ∆CDM (c-g-c)
b) Do ∆ABM = ∆CDM (cmt)
⇒ MAB = MCD (hai góc tương ứng)
⇒ MCD = 90⁰
⇒ MC ⊥ CD
⇒ AC ⊥ CD

