
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a,Áp dụng BĐT Cosi ta có:
\(a^2+\dfrac{1}{a^2}\ge2\sqrt{a^2.\dfrac{1}{a^2}}=2.1=2\)
dấu "=" xảy ra \(\Leftrightarrow a^2=\dfrac{1}{a^2} \Leftrightarrow a^4=1\Leftrightarrow a=\pm 1\)

a. Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{AM}=\left(x-1;y+1\right)\)
\(\overrightarrow{AM}=\overrightarrow{a}\Rightarrow\left\{{}\begin{matrix}x-1=3\\y+1=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=4\end{matrix}\right.\)
\(\Rightarrow M\left(4;4\right)\)
b. Do B thuộc Ox nên tọa độ có dạng: \(B\left(x;0\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(x-1;1\right)\)
\(\overrightarrow{AB}\) cùng phương \(\overrightarrow{a}\) khi: \(\dfrac{x-1}{3}=\dfrac{1}{5}\Rightarrow x=\dfrac{8}{5}\)
\(\Rightarrow B\left(\dfrac{8}{5};0\right)\)
c.
\(\overrightarrow{OA}=\left(1;-1\right)\Rightarrow T=1.3+\left(-1\right).5=-2\)
\(\Rightarrow cos\left(\overrightarrow{a},\overrightarrow{OA}\right)=\dfrac{\overrightarrow{a}.\overrightarrow{OA}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{OA}\right|}=\dfrac{-2}{\sqrt{1^2+\left(-1\right)^2}.\sqrt{3^2+5^2}}=-\dfrac{1}{\sqrt{17}}\)





1. TXĐ:
a. \(D=R\)
b. \(4x^2+5x-9\ne0\Rightarrow\left[{}\begin{matrix}x\ne1\\x\ne-\dfrac{9}{4}\end{matrix}\right.\) \(\Rightarrow D=R\backslash\left\{-\dfrac{9}{4};1\right\}\)
c. \(D=R\)
d. \(\left\{{}\begin{matrix}x+2\ne0\\x+4\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge-4\\x\ne-2\end{matrix}\right.\) \(\Rightarrow D=[-4;+\infty)\backslash\left\{-2\right\}\)
e. \(\left\{{}\begin{matrix}3-x\ge0\\x^2-5x+4\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\le3\\x\ne1\\x\ne4\end{matrix}\right.\) \(\Rightarrow D=(-\infty;3]\backslash\left\{1\right\}\)
f. \(\left\{{}\begin{matrix}x-1>0\\5-2x>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>1\\x< \dfrac{5}{2}\end{matrix}\right.\) \(\Rightarrow D=\left(1;\dfrac{5}{2}\right)\)
2.
\(1>0\Rightarrow f\left(1\right)=\dfrac{1+1}{1^2+1+1}=\dfrac{2}{3}\)
\(f\left(0\right)=0^2-2.0-1=-1\)
\(-2< 0\Rightarrow f\left(-2\right)=\left(-2\right)^2-2.\left(-2\right)-1=7\)


 giúp tớ câu c nhá
giúp tớ câu c nhá


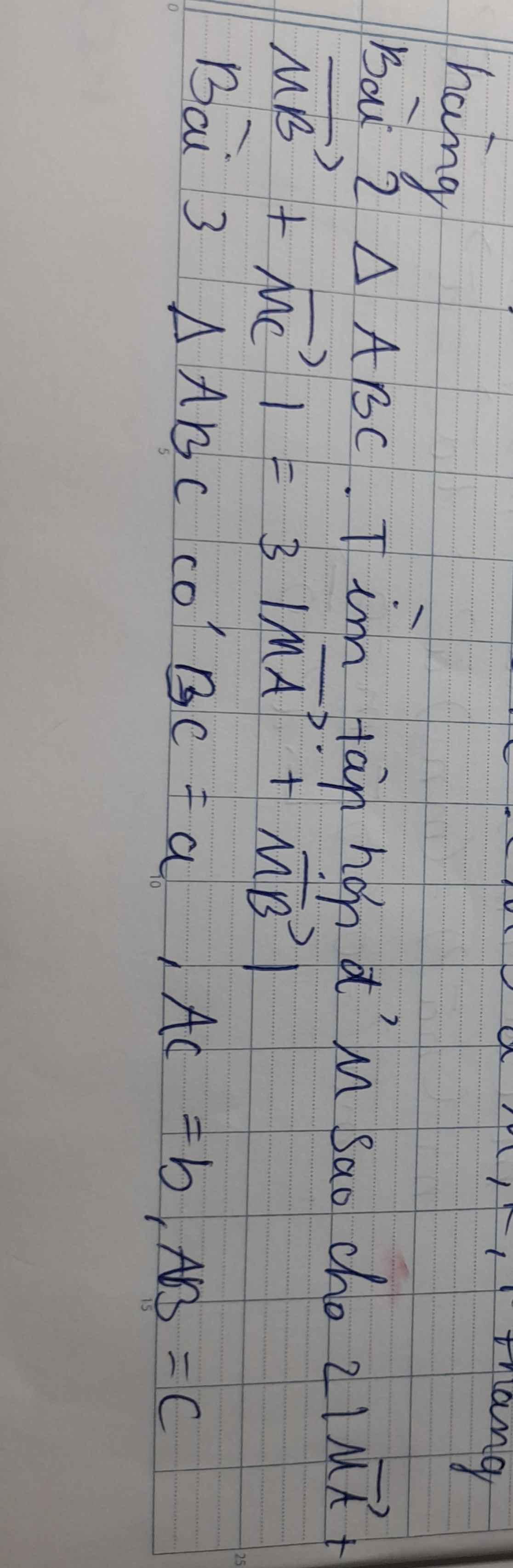
 giúp em bài này với ạ
giúp em bài này với ạ

 @@
@@